a) \(\dfrac{2^{12}\cdot5^7+4^6\cdot25^3}{8^5\cdot25^3+\left(2^2\cdot5^6\right)}\)
\(=\dfrac{2^{12}\cdot5^6\cdot5+\left(2^2\right)^6\cdot\left(5^2\right)^3}{\left(2^3\right)^5\cdot\left(5^2\right)^3+\left(2^2\right)^6\cdot5^6}\)
\(=\dfrac{2^{12}\cdot5^6\cdot5+2^{12}\cdot5^6}{2^3\cdot2^{12}\cdot5^6+2^{12}\cdot5^6}\)
\(=\dfrac{2^{12}\cdot5^6\cdot\left(5+1\right)}{2^{12}\cdot5^6\left(2^3+1\right)}\)
\(=\dfrac{6}{8+1}=\dfrac{6}{9}=\dfrac{2}{3}\)
b) \(\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}-\dfrac{5^{10}\cdot7^3-25^5\cdot49^2}{\left(125\cdot7\right)^3+5^9\cdot14^3}\)
\(=\dfrac{2^{12}\cdot3^5-\left(2^2\right)^6\cdot\left(3^2\right)^2}{\left(2^2\right)^6\cdot3^6+\left(2^3\right)^4\cdot3^5}-\dfrac{5^{10}\cdot7^3-\left(5^2\right)^5\cdot\left(7^2\right)^2}{\left(5^3\right)^3\cdot7^3+5^9\cdot7^3\cdot2^3}\)
\(=\dfrac{2^{12}\cdot3^4\cdot3-2^{12}\cdot3^4}{2^{12}\cdot3^4\cdot3^2+2^{12}\cdot3^4\cdot3}-\dfrac{5^9\cdot7^3\cdot5-5^9\cdot7^3\cdot5\cdot7}{5^9\cdot7^3+5^9\cdot7^3\cdot8}\)
\(=\dfrac{2^{12}\cdot3^4\cdot\left(3-1\right)}{2^{12}\cdot3^4\cdot\left(3^2+3\right)}-\dfrac{5^9\cdot7^3\cdot\left(5-35\right)}{5^9\cdot7^3\cdot\left(1+8\right)}\)
\(=\dfrac{3-1}{9+3}-\dfrac{5-35}{1+8}\)
\(=\dfrac{1}{6}-\dfrac{-30}{9}=\dfrac{7}{2}\)
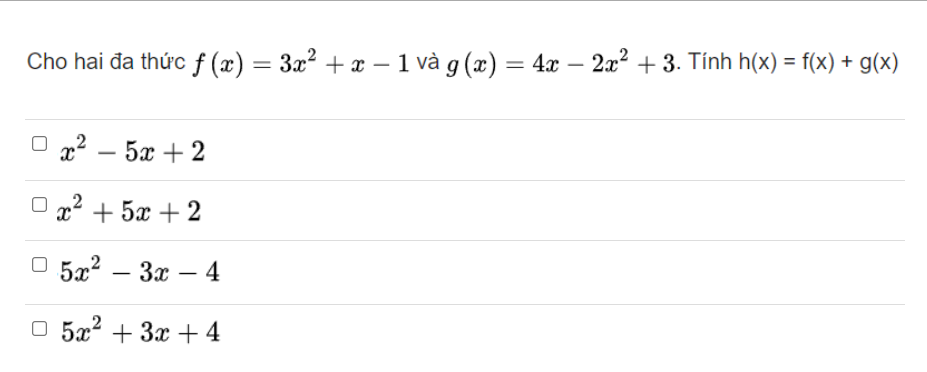
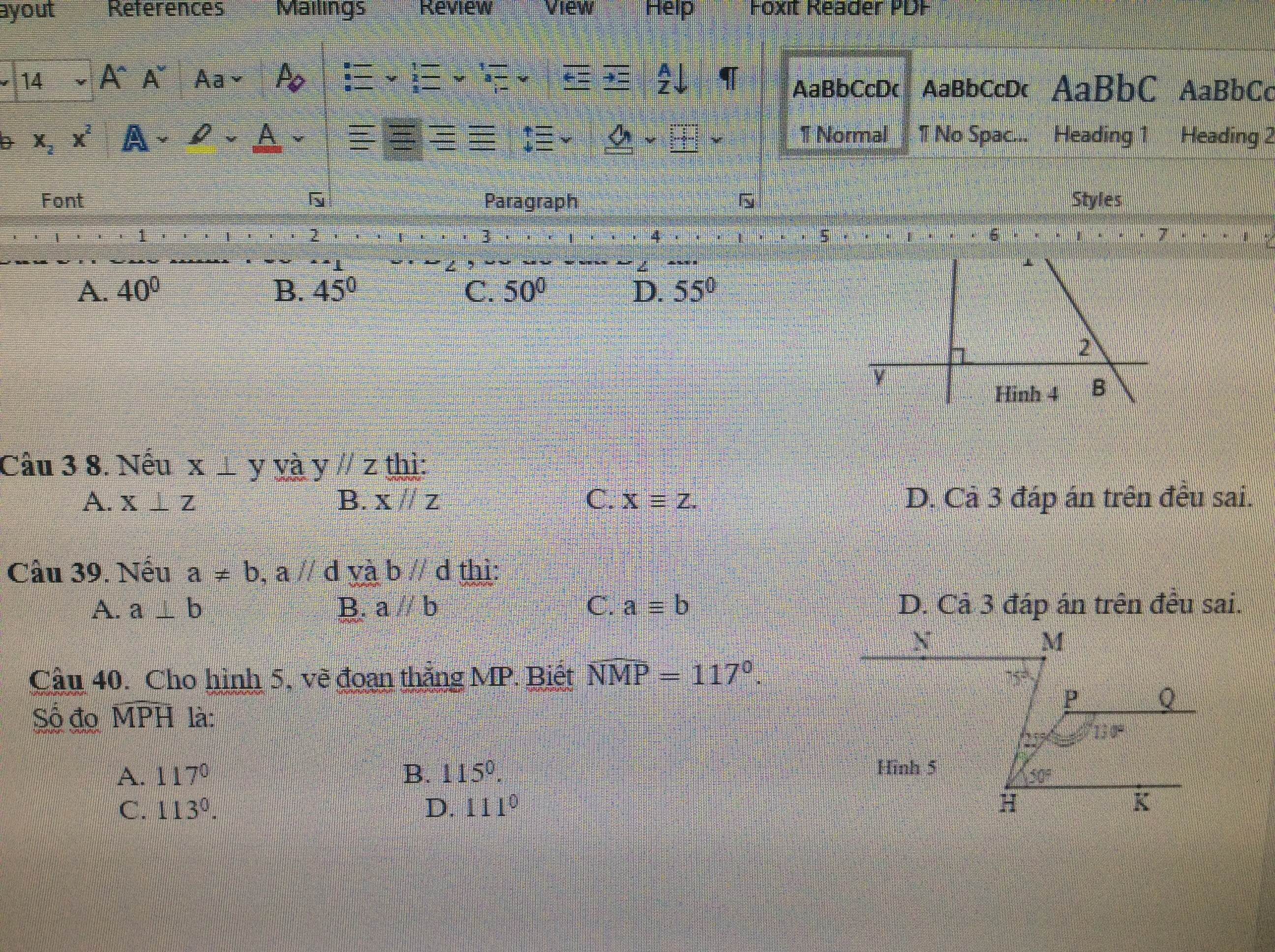Mik cần gấp ạaa
giúp em với em cần gấp ạaa
giúp em với ạaa
