12:
\(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{100}-1\right)\cdot\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{100}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{101}{100}\)
\(=\dfrac{-1}{100}\cdot\dfrac{101}{2}=\dfrac{-101}{200}< -0,5\)
11: 3C=1+1/3+...+1/3^98
=>2C=1-1/3^99
=>\(C=\dfrac{3^{99}-1}{2\cdot3^{99}}< \dfrac{1}{2}\)

















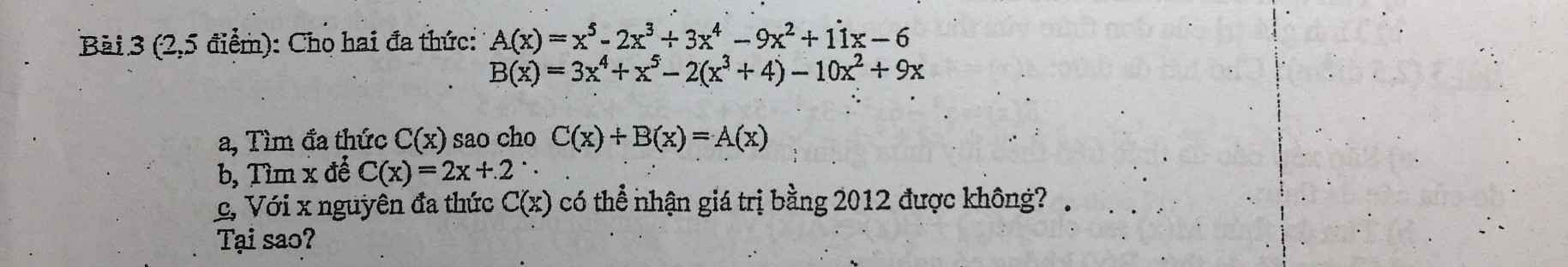 GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT
GIÚP MIK VỚI Ạ MIK CẦN GẤP !!! ÉT O ÉT

