Gọi MH là phân giác của góc BMC(H\(\in\)BC)
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ABC}+\widehat{ACB}=180^0-60^0=120^0\)
=>\(2\cdot\left(\widehat{MBC}+\widehat{MCB}\right)=120^0\)
=>\(\widehat{MBC}+\widehat{MCB}=\dfrac{120^0}{2}=60^0\)
Xét ΔBMC có \(\widehat{MBC}+\widehat{MCB}+\widehat{BMC}=180^0\)
=>\(\widehat{BMC}+60^0=180^0\)
=>\(\widehat{BMC}=180^0-60^0=120^0\)
Ta có: \(\widehat{FMB}+\widehat{BMC}=180^0\)(hai góc kề bù)
=>\(\widehat{FMB}=180^0-120^0=60^0\)
Ta có: \(\widehat{EMC}+\widehat{BMC}=180^0\)(hai góc kề bù)
=>\(\widehat{EMC}=180^0-120^0=60^0\)
Ta có: MH là phân giác của góc BMC
=>\(\widehat{BMH}=\widehat{CMH}=\dfrac{\widehat{BMC}}{2}=\dfrac{120^0}{2}=60^0\)
Xét ΔMHB và ΔMFB có
\(\widehat{HMB}=\widehat{FMB}\)
MB chung
\(\widehat{HBM}=\widehat{FBM}\)
Do đó: ΔMHB=ΔMFB
=>MH=MF
Xét ΔMHC và ΔMEC có
\(\widehat{HMC}=\widehat{EMC}\)
MC chung
\(\widehat{MCH}=\widehat{MCE}\)
Do đó: ΔMHC=ΔMEC
=>MH=ME
mà MH=MF
nên ME=MF

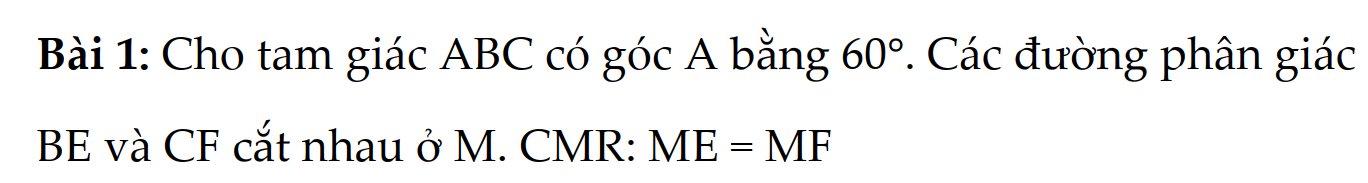 em mới học hết tam giác mn giúp em vs ạ
em mới học hết tam giác mn giúp em vs ạ











