Các câu hỏi tương tự
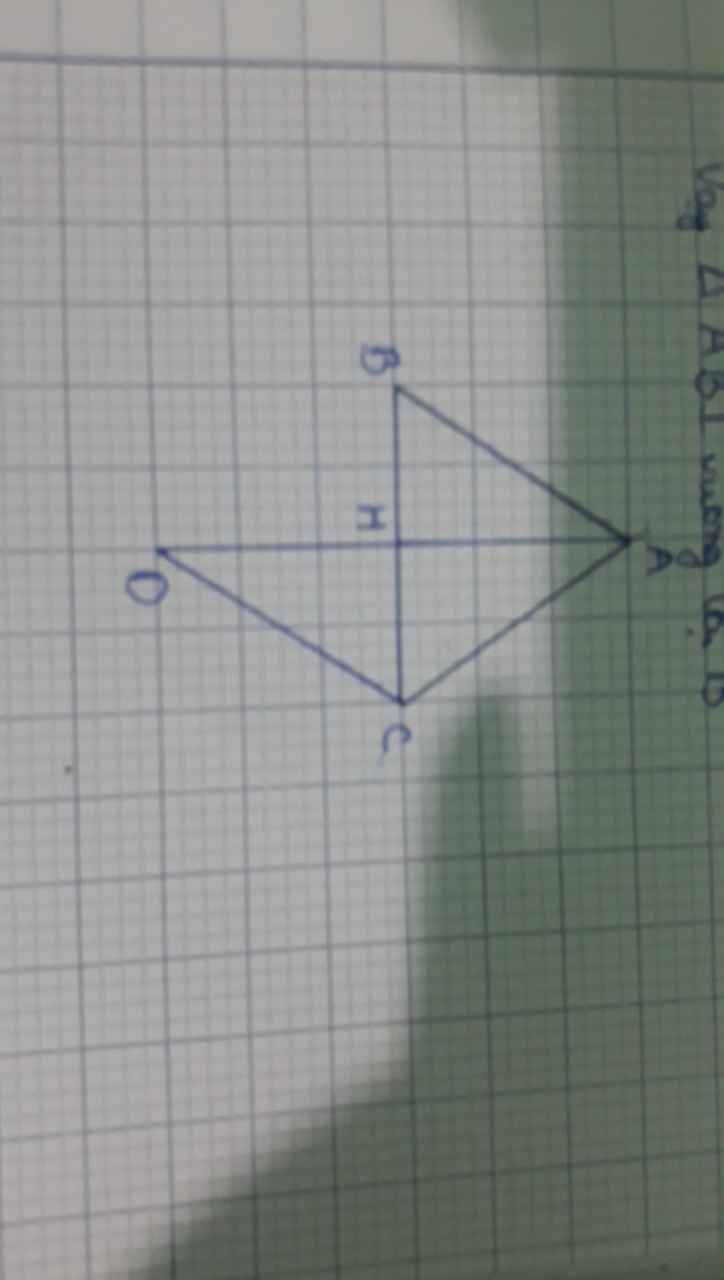
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD HA. Trên tia đối của tia CB lấy điểm E sao cho CECB. a) Chứng minh: Tam giác ACD cân b) Chứng minh: Tam giác ACETam giác DCE c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC 2DK Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD HA. Trên tia đối của tia CB lấy điểm E sao cho CECB.a) Chứng minh: Tam giác ACD cânb) Chứng minh: Tam giác ACETam...
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD= HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB. a) Chứng minh: Tam giác ACD cân b) Chứng minh: Tam giác ACE=Tam giác DCE c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC> 2DK Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điêm D sao cho HD= HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB.
a) Chứng minh: Tam giác ACD cân
b) Chứng minh: Tam giác ACE=Tam giác DCE
c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC> 2DK
cho tam giác ABC vuông tại A vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HD=HA.
a) Chứng minh tam giac AHC= tam giac DHC
b) Cho BC =10cm;AB=6cm. Tính độ dài cạnh AC
c) Trên HC lấy điểm E sao cho HE=HB. Chứng minh tam giác AHB= tam giác DHE và DE vuông góc với AC.
d) Chứng minh AE+CD>BC
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điểm D sao cho HD=HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB. a) Chứng minh: AC=DC. b) Chứng minh: Tam giác ACE=Tam giác DCE. c) Đường thẳng AC cắt DE tại K. Chứng minh: AB+BC>2DK
Bài 2. Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
a) Chứng minh: tam giác AHB = tam giác AHC .
b) Trên tia đối của tia HA, lấy điểm K sao cho HK= HA. Chứng minh: tam giác AHB = tam giác KHC .
c) Chứng minh: tam giác ACK là tam giác cân.
d) Qua A kẻ đường thẳng song song với BC, cắt CK tại I. Chứng minh: KI = 2AC.
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điểm D sao cho điểm HD=HA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
a/ chứng minh AC=DC
b/ chứng minh tam giác ACE = tam giác DCE
c/ Đường thẳng AC cắt DE tại K. Chưng minh AB+BC>2DK
Cho tam giác ABC có 3 góc nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD.
a) Chứng minh: tam giác AHB = tam giác DHB
b) Chứng minh rằng: BC là tia phân giác của góc ABD
c) Gọi M là trung điểm của Bc. Trên tia đối của tia MA lấy điểm F sao cho MF = MA. Từ F kẻ FN vuông góc với BC (N thuộc BC). Chứng minh: HD = NF
Cho tam giác ABC có ba góc nhọn ( AB < AC ) . Kẻ AH vuông góc với BC tại H. Trên đoạn thẳng HC lấy điểm E sao cho HE = HB
a) Chứng minh tam giác AHB = tam giác AHE
b) Trên tia đối tia HA lấy điểm D sao cho HD = HA . Chứng minh DE P AB
c) Chứng minh EAC = EDC
d) Tia DE cắt AC tại M . Từ M kẻ đường thẳng song song với AD cắt DC tại N . Chứng minh A,E,N thẳng hàng
Cho tam giác ABC vuông tại A (AB<AC). Đường cao AH; trên tia HC lấy D sao cho HB=HD.
a) Chứng minh tam giác ABH= tam giác ADH
b) Trên tia đối của tia HA lấy E sao cho HA=HE. Chứng minh tam giác DEA cân
c) Chứng minh BC-BD>AC-AB.
d) Kẻ CK vuông với AD tại K. Chứng minh AH; BE; CK đồng quy
Cho tam giác ABC vuông tại A, AB < AC, đường cao AH ( H thuộc BC). Trên tia tia đối của tia HA lấy M sao cho HM = HA. Trên tia đối của tia HB lấy D sao cho HD = HB
a) Chứng minh: tam giác AHB = tam giác MHD
b) Chứng minh: AB//MD; MD vuông góc AC
c) Gọi E là trung điểm của AB, F là trung điểm của MD. Chứng minh: E, H, F thẳng hàng