c: Đặt \(\sqrt[3]{2x-1}=a;\sqrt[3]{x-1}=b\)
Phương trình sẽ là \(a+b=\sqrt[3]{3x-2}\)
\(\Leftrightarrow\left(a+b\right)^3=3x-2\)
\(\Leftrightarrow3x-2+3ab\left(a+b\right)=3x-2\)
\(\Leftrightarrow ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x-1=0\\\sqrt[3]{2x-1}=-\sqrt[3]{x-1}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=1\\2x-1=1-x\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{1}{2};1;\dfrac{3}{2}\right\}\)
d: Đặt \(\sqrt[3]{x+5}=a;\sqrt[3]{x+6}=b\)
Phương trình sẽ là \(a+b=\sqrt[3]{a^3+b^3}\)
\(\Leftrightarrow\left(a+b\right)^3=a^3+b^3\)
=>3ab(a+b)=0
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\x+6=0\\x+5=-x-6\end{matrix}\right.\Leftrightarrow x\in\left\{-5;-6;-\dfrac{11}{2}\right\}\)
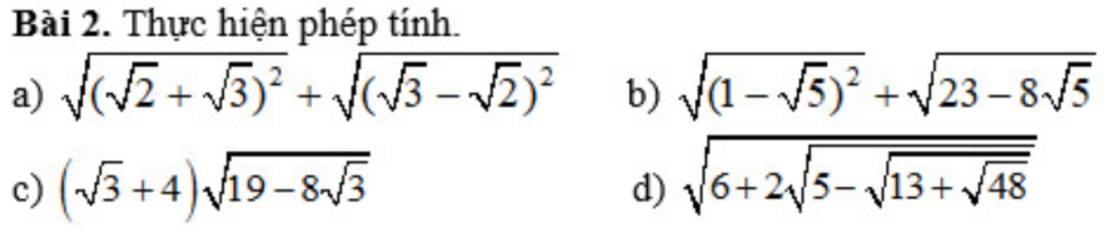câu b, c, d thôi ạ!
