Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
Bài 1 : Dùng hằng đẳng thức để khai triển và thu gọn các biểu thức sau
a) \(\left(-4xy-5\right).\left(5-4xy\right)\)
b) \(\left(a^2b+ab^2\right).\left(ab^2-a^2b\right)\)
c) \(\left(3x-4\right)^2+2.\left(3x-4\right).\left(4-x\right)+\left(4-x\right)^2\)
d) \(\left(a^2+ab+b^2\right).\left(a^2-ab+b^2\right)-\left(a^4+b^4\right)\)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau a /(x+y)^3-,(x-y)^3;. b/(2y-3)^3
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau. A/. (x+y)^3-(x-y)^3
Dùng hẳng đẳng thức để khai triển và thu gọn
a) (6x+5y) ( 6x-5y)
b) (-4xy-5)(5-4xy)
c) (3x-4)^2 +2.(3x - 4 ) . ( 4-x ) + (4-x)^2
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau (1phần 3y+3)^3
Dùng hằng đẳng thức để triển khai và thu gọn
\(3x^2\left(x+1\right)\left(x-1\right)+\left(x^2-1\right)^3-\left(x^2-1\right)\left(x^4+x^2+1\right)\)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau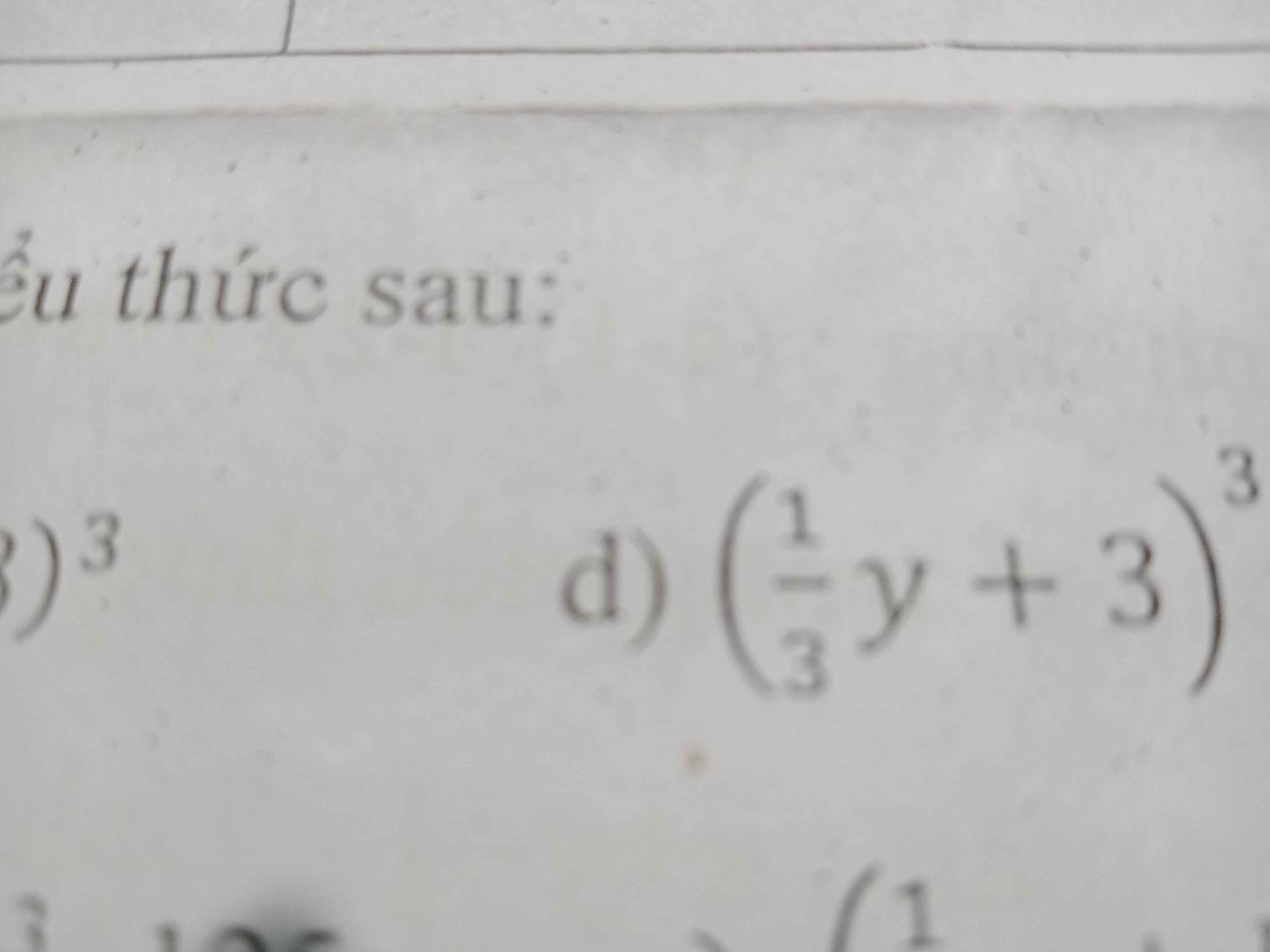
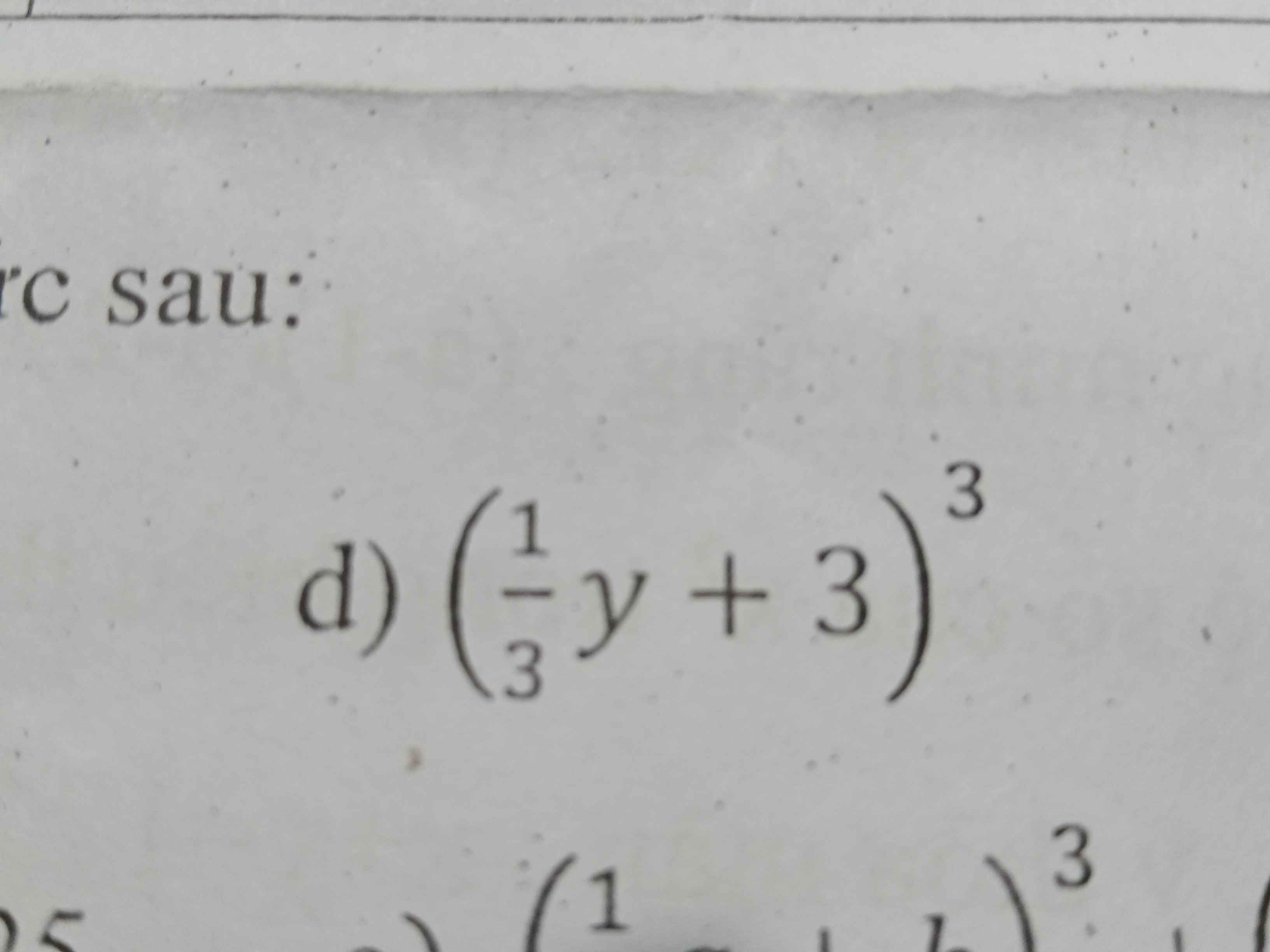
Trong các khai triển hằng đẳng thức sau, khai triển nào sai?
A.(A + B)^2=A^2+2AB+B^2
B.(A + B)^3=A^2+2A^2B+2AB^2+B^3
C.(A - B)^2=A^2-2AB+B^2
D.(A - B)^2=A^3-3A^2B+3AB^2-B^3