Các câu hỏi tương tự
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số: y = – x 4 – x 2 + 6
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng: y = x/6 –1
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:y −
x
3
+ 3x + 1b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:y
(
x
+
1
)
3
− 3x − 4c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
(
x
+
1...
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
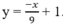
Cho hàm số
y
2
x
-
1
x
-
1
có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị a+ b bằng A. 3 B . 4 C. 5 D. 6
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và điểm I (1; 2). Điểm M( a; b) ; a> 0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM.
Giá trị a+ b bằng
A. 3
B . 4
C. 5
D. 6
Gọi (C) là đồ thị của hàm số
y
x
4
+
x
Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng d:x+5y0 có phương trình là A. B. C. D.
Đọc tiếp
Gọi (C) là đồ thị của hàm số y = x 4 + x Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng d:x+5y=0 có phương trình là
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
y
1
3
x
3
-
2
x
2
+
2
x
+
1
C
. Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h. A.
h
2
B.
h
4
2
3...
Đọc tiếp
Cho hàm số y = 1 3 x 3 - 2 x 2 + 2 x + 1 C . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d: y = x. Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
A. h = 2
B. h = 4 2 3
C. h = 2 3
D. h = 2 2 3
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: yx+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất. A. m-1. B.m-2 . C. m3 . D. m-5.
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y=x+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất.
A. m=-1.
B.m=-2 .
C. m=3 .
D. m=-5.
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: y x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất. A. -2 B. -1 C. 1 D. 2
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
A. -2
B. -1
C. 1
D. 2







