Các câu hỏi tương tự
Cho hàm số
f
x
x
+
2
x
2
-
9
có đồ thị như trên hình 53.a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x...
Đọc tiếp
Cho hàm số f x = x + 2 x 2 - 9 có đồ thị như trên hình 53.
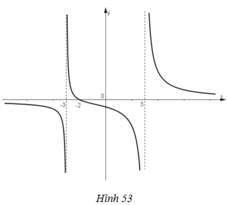
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x → - ∞ , x → 3 - , x → - 3 +
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = |sin x|
Cho hàm số y
x
3
+
2
m
+
1
x
2
+
3
m
x
+
2
có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng
2
6
A. m -2 B. m -2 hoặc m 3 C. m 3 D. K...
Đọc tiếp
Cho hàm số y = x 3 + 2 m + 1 x 2 + 3 m x + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y = -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6
A. m = -2
B. m = -2 hoặc m = 3
C. m = 3
D. Không tồn tại m
Cho hàm số f(x) có đồ thị như hình dưới đây:- Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ? A.
lim
x
→
-
∞
f
x
B.
lim
x
→
+
∞
f
x
C.
lim
x...
Đọc tiếp
Cho hàm số f(x) có đồ thị như hình dưới đây:
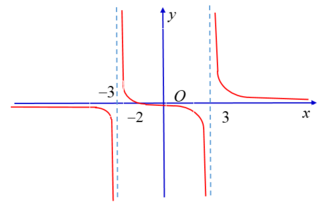
- Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?
A. lim x → - ∞ f x
B. lim x → + ∞ f x
C. lim x → - 3 + f x
D. l i m x → - 3 - f x
Cho hàm số f(x) có đồ thị như hình dưới đây: Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?
Đọc tiếp
Cho hàm số f(x) có đồ thị như hình dưới đây:
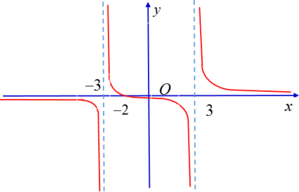
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?
![]()
![]()
![]()
![]()
Cho hai hàm số
f
(
x
)
x
2
và có
g
x
-
x
2
+
2
...
Đọc tiếp
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
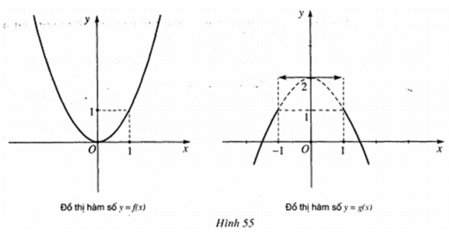
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
tìm m thỏa mãn yêu cầu bài toána) đồ thị hàm số ydfrac{x+3}{2x+3m} có đường tiệm cận đứng đi qua điểm M (3;-1)b) đường thẳng x -2 là tiệm cận đứng của đồ thị hàm số ydfrac{2x-3}{x+m}c) biết đồ thị hàm số ydfrac{ax+1}{bx-2} có tiệm cận đứng là x 2 và tiệm cận ngang y 3. Tính 2a+3bd) đồ thị hàm số ydfrac{x+2}{x^2+2x+m^2-3m} có 2 đường tiệm cận đứng
Đọc tiếp
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) có đường tiệm cận đứng đi qua điểm M (3;-1)
b) đường thẳng x = -2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
c) biết đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có tiệm cận đứng là x = 2 và tiệm cận ngang y = 3. Tính 2a+3b
d) đồ thị hàm số \(y=\dfrac{x+2}{x^2+2x+m^2-3m}\) có 2 đường tiệm cận đứng
Dựa trên đồ thị hàm số y = sin x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.
tìm m thỏa mãn yêu cầu bài toána) đồ thị hàm số ydfrac{mx-1}{2x+m} có đường tiệm cận đứng đi qua điểm A (-1;sqrt{2})b) đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số ydfrac{x-2}{2x-m}c) biết đồ thị hàm số ydfrac{left(m+1right)x+2}{x-n+1} nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+nd) đồ thị hàm số ydfrac{x-1}{x^2+2left(m-1right)x+m^2-2} có 2 đường tiệm cận đứng
Đọc tiếp
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\) có đường tiệm cận đứng đi qua điểm A (-1;\(\sqrt{2}\))
b) đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
c) biết đồ thị hàm số \(y=\dfrac{\left(m+1\right)x+2}{x-n+1}\) nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+n
d) đồ thị hàm số \(y=\dfrac{x-1}{x^2+2\left(m-1\right)x+m^2-2}\) có 2 đường tiệm cận đứng