Các câu hỏi tương tự
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
2
x
-
1
2
trục hoành, đường thẳng
x
2
và đường thẳng
x
3
A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 2 x - 1 2 trục hoành, đường thẳng x = 2 và đường thẳng x = 3
A. 3
B. 2
C. 1
D. 4
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
2
(
x
-
1
)
2
, trục hoành và các đường thẳng x2 và x8 A.
12
7
B. 12 C. 9 D. 10
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 2 ( x - 1 ) 2 , trục hoành và các đường thẳng x=2 và x=8
A. 12 7
B. 12
C. 9
D. 10
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
ln
x
, trục Ox và đường thẳng xe A.
S
e
2
+
3
4
B.
S
e
2
-...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x ln x , trục Ox và đường thẳng x=e
A. S = e 2 + 3 4
B. S = e 2 - 1 2
C. S = e 2 + 1 2
D. S = e 2 + 1 4
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = 3 x 2 + 1 , trục hoành và hai đường thẳng x = 0, x = 2 là
A. S = 8
B. S = 12
C. S = 10
D. S = 9
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số
y
1
-
1
x
2
, trục hoành và đường thẳng x 1 và đường thẳng x 2 A. 0,3 B. 0,2 C. 0,4 D. 0,5
Đọc tiếp
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 1 - 1 x 2 , trục hoành và đường thẳng x = 1 và đường thẳng x = 2
A. 0,3
B. 0,2
C. 0,4
D. 0,5
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
y
x
3
-
4
x
, trục hoành và hai đường thẳng x -2, x4 là A. S 44 B. S 8. C. S 22 D. S36
Đọc tiếp
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 3 - 4 x , trục hoành và hai đường thẳng x= -2, x=4 là
A. S =44
B. S =8.
C. S =22
D. S=36
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
-
3
x
+
2
trục hoành và hai đường thẳng x1,x2 Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng A. π/30 B. π/6 C. 1/6 D. 1/30
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 3 x + 2 trục hoành và hai đường thẳng x=1,x=2 Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng
A. π/30
B. π/6
C. 1/6
D. 1/30
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
x
3
, trục hoành và hai đường thẳng x -1, x 2, biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm. A. 15 (
c
m
2
) B.
15
4
(
c
m
2
)
C.
17
4
(...
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 3 , trục hoành và hai đường thẳng x = -1, x = 2, biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm.
A. 15 ( c m 2 )
B. 15 4 ( c m 2 )
C. 17 4 ( c m 2 )
D. 17 ( c m 2 )
Cho hàm số yf(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x0,x2 (phần tô đen) là A.
S
-
∫
0
1
f
x
d
x
+
∫
1
2
f
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích hình phẳng giới hạn bởi đồ thị (C), trục hoành và hai đường thẳng x=0,x=2 (phần tô đen) là
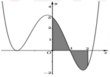
A. S = - ∫ 0 1 f x d x + ∫ 1 2 f x d x
B. S = ∫ 0 1 f x d x - ∫ 1 2 f x d x
C. S = ∫ 0 2 f x d x
D. S = ∫ 0 2 f x d x