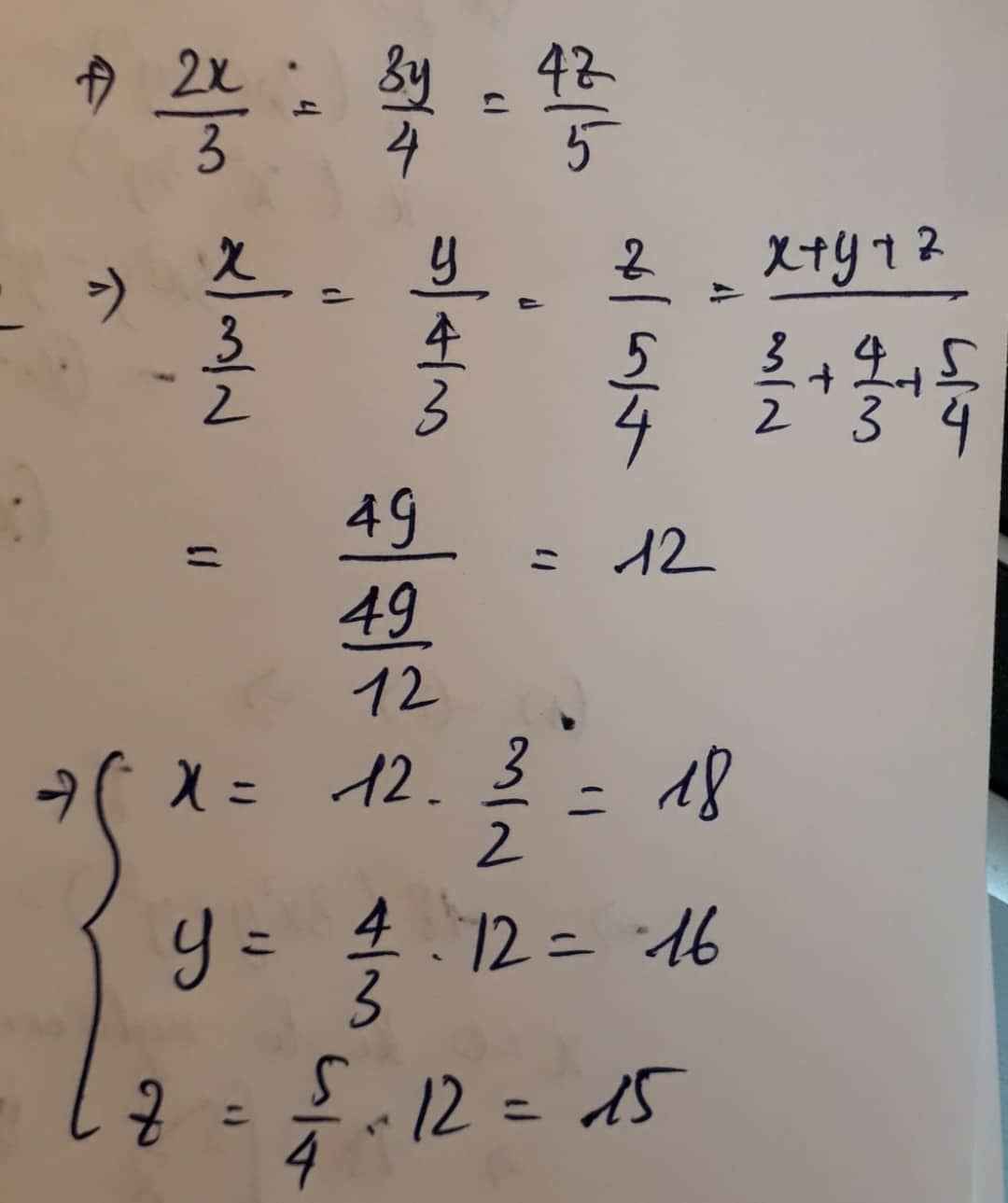Ta có \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)
=> \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)=\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
Theo tính chất của dãy tỉ số bằng nhau ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)=\(\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}\)=12
=> x = \(\dfrac{3}{2}.12=18\)
y=12. 4/3=16
z= 12. 5/4= 15
Ta có:
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)
\(=>\dfrac{12x}{18}=\dfrac{12y}{16}=\dfrac{12z}{15}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{12x}{18}=\dfrac{12y}{16}=\dfrac{12z}{15}=\)\(\dfrac{12x+12y+12z}{18+16+15}=\dfrac{12\left(x+y+z\right)}{18+16+15}=\dfrac{12.49}{49}=12\)
\(\dfrac{12x}{18}=12=>12x=216\)
\(\dfrac{12y}{16}=12=>12y=192\)
\(\dfrac{12z}{15}=12=>12z=180\)
=> \(x=18;y=16;z=15\)