Đáp án C
Ta có: y ' = 3 e x . ln 3 e x ' = e x .3 e x ln 3
Đáp án C
Ta có: y ' = 3 e x . ln 3 e x ' = e x .3 e x ln 3
Cho hàm số y = 2 ln ln x - ln 2 x . Tính giá trị của y'(e)
A. 1 e
B. 2 e
C. e 2
D. 1 2 e
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x = ln(x) trên đoạn 1 2 ; e lần lượt là
A. 1 và e - 1
B. 1 và e
C. 1 2 + ln 2 và e - 1
D. 1 và 1 2 + ln 2
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x ln x , trục Ox và đường thẳng x=e
A. S = e 2 + 3 4
B. S = e 2 - 1 2
C. S = e 2 + 1 2
D. S = e 2 + 1 4
Tính đạo hàm của hàm số y = 3 . e - x + 2017 e c o s x
A. y ' = - 3 . e - x + 2017 s i n x . e c o s x
B. y ' = - 3 . e - x - 2017 s i n x . e c o s x
C. y ' = 3 . e - x - 2017 s i n x . e c o s x
D. y ' = 3 . e - x + 2017 s i n x . e c o s x
\(\int\limits^{ln\sqrt{3}}_0\frac{dx}{e^x+e^{-x}}\)
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
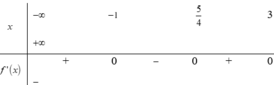
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Giá trị nhỏ nhất của hàm số y = ln x x trên đoạn [1;e] bằng:
A. 0
B. 1
C. - 1 e
D. e