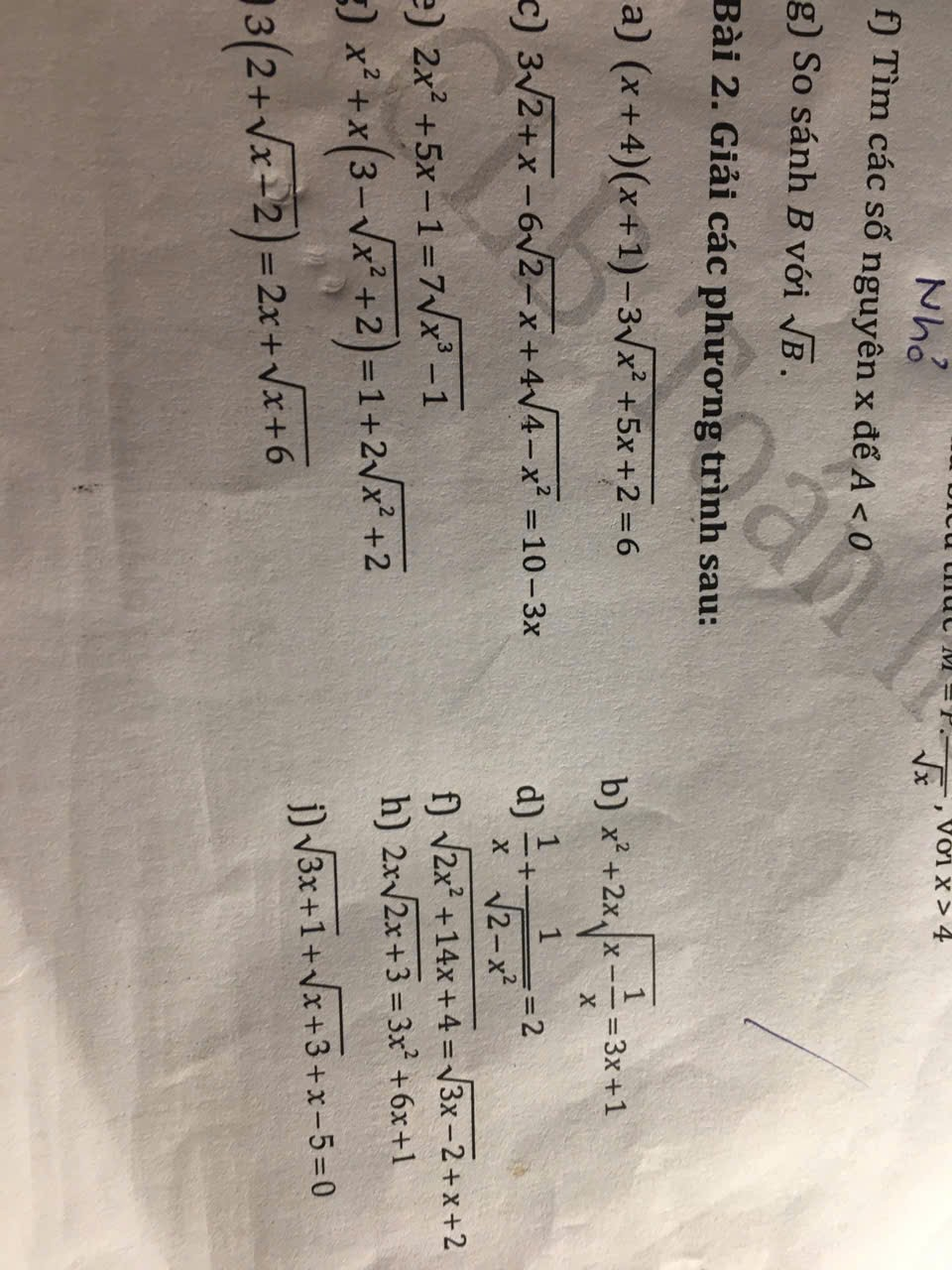a: ĐKXĐ: \(x^2+5x+2\ge0\)
=>\(x^2+2\cdot x\cdot\frac52+\frac{25}{4}-\frac{17}{4}\ge0\)
=>\(\left(x+\frac52\right)^2\ge\frac{17}{4}\)
=>\(\left[\begin{array}{l}x+\frac52\ge\frac{\sqrt{17}}{2}\\ x+\frac52\le-\frac{\sqrt{17}}{2}\end{array}\right.\Rightarrow\left[\begin{array}{l}x\ge\frac{\sqrt{17}-5}{2}\\ x\le\frac{-\sqrt{17}-5}{2}\end{array}\right.\)
\(\left(x+4\right)\left(x+1\right)-3\cdot\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\cdot\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\cdot\sqrt{x^2+5x+2}-4=0\)
=>\(\left(\sqrt{x^2+5x+2}-4\right)\left(\sqrt{x^2+5x+2}+1\right)=0\)
mà \(\sqrt{x^2+5x+2}+1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x^2+5x+2}-4=0\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>(x+7)(x-2)=0
=>\(\left[\begin{array}{l}x=-7\left(nhận\right)\\ x=2\left(nhận\right)\end{array}\right.\)
d: ĐKXĐ: \(\begin{cases}2-x^2\ge0\\ x<>0\end{cases}\Rightarrow\begin{cases}x^2\le2\\ x<>0\end{cases}\Rightarrow\begin{cases}-\sqrt2\le x\le\sqrt2\\ x<>0\end{cases}\)
Ta có: \(\frac{1}{x}+\frac{1}{\sqrt{2-x^2}}=2\)
=>\(\left(\frac{1}{x}-1\right)+\left(\frac{1}{\sqrt{2-x^2}}-1\right)=0\)
=>\(\frac{1-x}{x}+\frac{1-\sqrt{2-x^2}}{\sqrt{2-x^2}}=0\)
=>\(\frac{x-1}{x}+\frac{\sqrt{2-x^2}-1}{\sqrt{2-x^2}}=0\)
=>\(\frac{x-1}{x}+\frac{2-x^2-1}{\sqrt{2-x^2}\cdot\left(\sqrt{2-x^2}+1\right)}=0\)
=>\(\frac{x-1}{x}+\frac{1-x^2}{\sqrt{2-x^2}\cdot\left(\sqrt{2-x^2}+1\right)}=0\)
=>\(\frac{x-1}{x}-\frac{\left(x-1\right)\left(x+1\right)}{\sqrt{2-x^2}\cdot\left(\sqrt{2-x^2}+1\right)}=0\)
=>\(\left(\frac{1}{x}-\frac{\left(x+1\right)}{\sqrt{2-x^2}\cdot\left(\sqrt{2-x^2}+1\right)}\right)\cdot\left(x-1\right)=0\)
=>x-1=0
=>x=1(nhận)
j: ĐKXĐ: \(\begin{cases}3x+1\ge0\\ x+3\ge0\end{cases}\Rightarrow\begin{cases}x\ge-\frac13\\ x\ge-3\end{cases}\Rightarrow x\ge-\frac13\)
Ta có: \(\sqrt{3x+1}+\sqrt{x+3}+x-5=0\)
=>\(\sqrt{3x+1}-2+\sqrt{x+3}-2+x-1=0\)
=>\(\frac{3x+1-4}{\sqrt{3x+1}+2}+\frac{x+3-4}{\sqrt{x+3}+2}+\left(x-1\right)=0\)
=>\(\frac{3x-3}{\sqrt{3x+1}+2}+\frac{x-1}{\sqrt{x+3}+2}+\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\frac{3}{\sqrt{3x+1}+2}+\frac{1}{\sqrt{x+3}+2}+1\right)=0\)
=>x-1=0
=>x=1(nhận)
i:
ĐKXĐ: \(\begin{cases}x-2\ge0\\ x+6\ge0\end{cases}\Rightarrow\begin{cases}x\ge2\\ x\ge-6\end{cases}\Rightarrow x\ge2\)
ta có: \(3\left(2+\sqrt{x-2}\right)=2x+\sqrt{x+6}\)
=>\(6+3\sqrt{x-2}=2x+\sqrt{x+6}\)
=>\(6+3\sqrt{x-2}-3=2x+\sqrt{x+6}-3\)
=>\(6+3\cdot\left(\sqrt{x-2}-1\right)=2x+\frac{x+6-9}{\sqrt{x+6}+3}\)
=>\(6+3\cdot\frac{x-2-1}{\sqrt{x-2}+1}=2x+\frac{x-3}{\sqrt{x+6}+3}\)
=>\(2x+\frac{x-3}{\sqrt{x+6}+3}-6-3\cdot\frac{\left(x-3\right)}{\sqrt{x-2}+1}=0\)
=>\(\left(x-3\right)\left(2+\frac{x-3}{\sqrt{x+6}+3}-\frac{3}{\sqrt{x-2}+1}\right)=0\)
=>x-3=0
=>x=3(nhận)