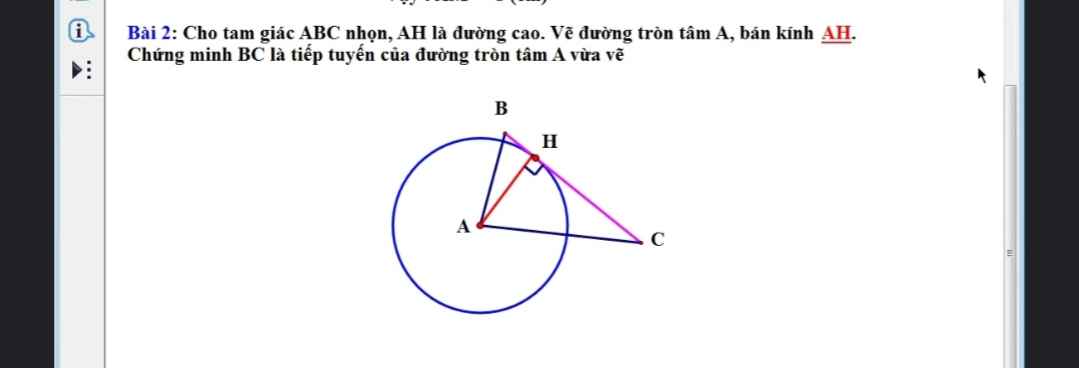
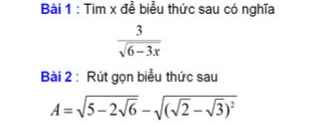Lời giải:
$x^2+y^2=z^2\Rightarrow (\frac{x}{z})^2+(\frac{y}{z})^2=1$
Đặt $\frac{x}{z}=a; \frac{y}{z}=b$ thì bài toán trở thành:
Cho $a,b>0$ thỏa mãn: $a^2+b^2=1$.
Tìm min $P=(1+\frac{1}{a})(1+\frac{1}{b})$
------------------
Có:
Áp dụng BĐT Cô-si: $1=a^2+b^2\geq 2ab$
$P=\frac{(a+1)(b+1)}{ab}=\frac{a+b+ab+1}{ab}=\frac{a+b+ab+a^2+b^2}{ab}$
$\geq \frac{2\sqrt{ab}+ab+2ab}{ab}$
$=\frac{2\sqrt{ab}+3ab}{ab}$
Vì $1\geq 2ab\Rightarrow 1\geq \sqrt{2ab}$
$\Rightarrow P\geq \frac{2\sqrt{2ab}.\sqrt{ab}+3ab}{ab}=\frac{(2\sqrt{2}+3)ab}{ab}=2\sqrt{2}+3$
Vậy $P_{\min}=2\sqrt{2}+3$
Đúng 1
Bình luận (0)