\(\text{#TNam}\)
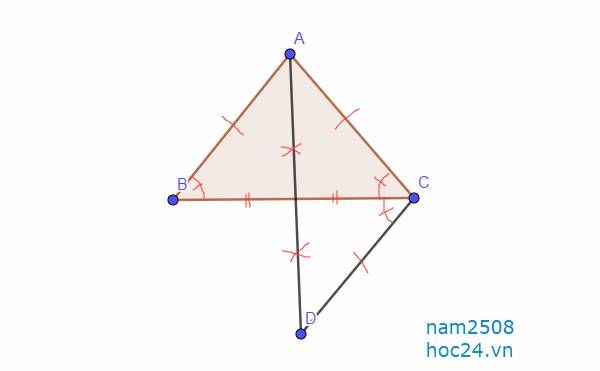
`a,` Vì Tam giác `ABC` cân tại `A -> AB=AC,` \(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABM` và Tam giác `ACM:`
`AB=AC (CMT)`
\(\widehat{B}=\widehat{C}\)
`MB=MC (g``t)`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`b,` Xét Tam giác `AMB` và Tam giác `CMD:`
`AM=MD (g``t)`
\(\widehat{AMB}=\widehat{CMD}\) `( \text {2 góc đối đỉnh})`
`MB = MC (g``t)`
`=> \text {Tam giác AMB = Tam giác CMD (c-g-c)}`
`->`\(\widehat{ABC}=\widehat{DCB}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong
`-> \text {AB // CD}`
`c,` Vì Tam giác `AMB =` Tam giác `CMD (b)`
`-> AB=CD (\text {2 cạnh tương ứng})`
Mà `AB = AC (a)`
`-> AC = CD`
Xét Tam giác `ACD: AC = CD`
`-> \text {Tam giác ACD cân tại C}`