1: \(=\left[\left(\sqrt{2}+\sqrt{3}\right)^2-5\right]\cdot\left[\left(\sqrt{5}\right)^2-\left(\sqrt{2}-\sqrt{3}\right)^2\right]\)
\(=2\sqrt{6}\left(5-5+2\sqrt{6}\right)=2\sqrt{6}\cdot2\sqrt{6}=24\)
2: \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
=>\(A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\cdot\sqrt{16-10-2\sqrt{5}}\)
\(=8+2\cdot\sqrt{6-2\sqrt{5}}\)
\(=8+2\left(\sqrt{5}-1\right)=6+2\sqrt{5}\)
=>\(A=\sqrt{5}+1\)

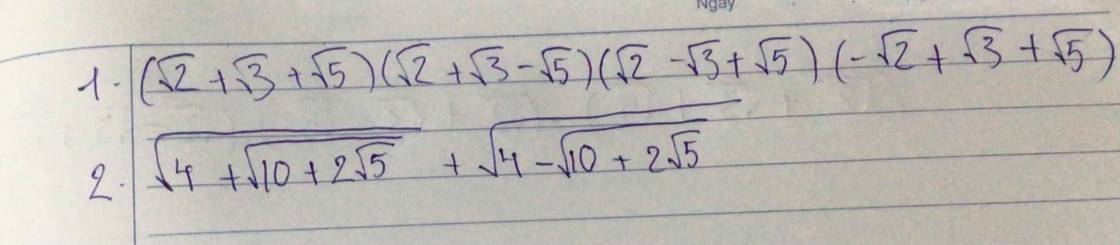







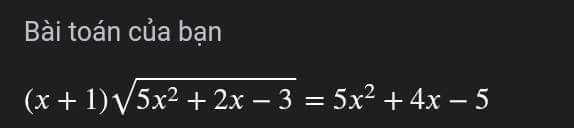



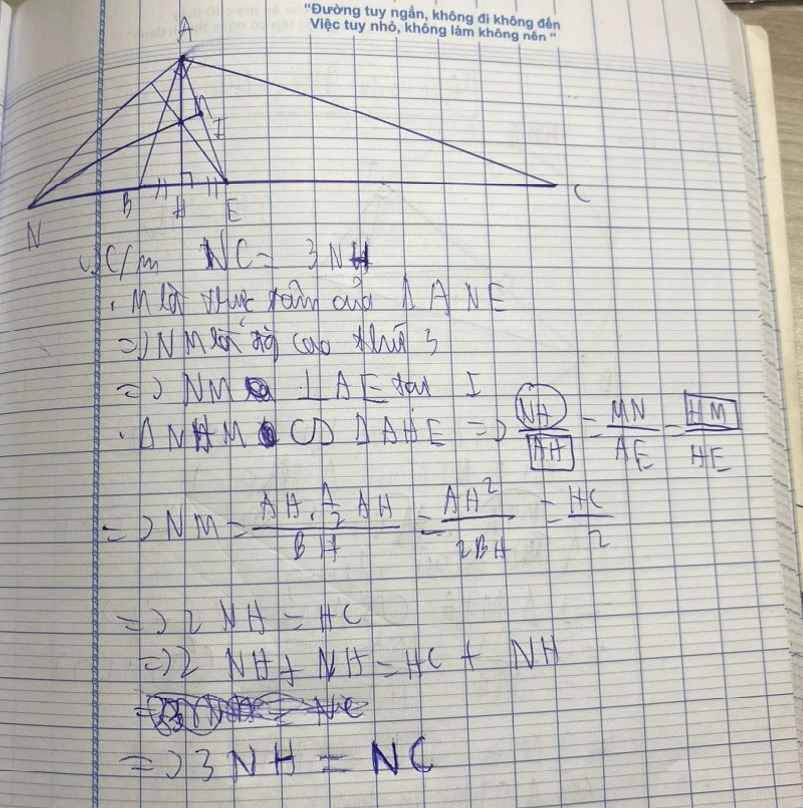 bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ
bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ





 Trừ bài 8, 14,15, 13. Còn lại ai lm đc bài nào giúp tui với
Trừ bài 8, 14,15, 13. Còn lại ai lm đc bài nào giúp tui với 