Các câu hỏi tương tự
Chứng minh rằng f′(x) 0 ∀x ∈ R , nếu:
f
(
x
)
3
(
sin
4
x
+
cos
4
x
)
−
2
(
sin
6
x
+
cos
6
x
)
Đọc tiếp
Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = 3 ( sin 4 x + cos 4 x ) − 2 ( sin 6 x + cos 6 x )
Cho các hàm số
f
x
sin
4
x
+
cos
4
x
,
g
x
sin
6
x
+
cos
6
x
. Tính biểu thức:
3
f
x
-
2
g
x...
Đọc tiếp
Cho các hàm số f x = sin 4 x + cos 4 x , g x = sin 6 x + cos 6 x . Tính biểu thức: 3 f ' x - 2 g ' x + 2
A.0
B.1
C.2
D.3
Tìm số nghiệm của phương trình sin8x + cos4x = 1 + 2sin2x cos6x thuộc - π ; π
A. 6
B. 5
C.7
D.9
sin
6
x
+
cos
6
x
cos
4
x
phương trình nào sau đây tương đương với phương trình vừa cho:
Đọc tiếp
sin 6 x + cos 6 x = cos 4 x phương trình nào sau đây tương đương với phương trình vừa cho:
![]()
![]()
![]()
![]()
Đạo hàm của hàm số y cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây? A.
-
6
cos
5
x
sin
x
B.
6
cos
5
x
sin
x
C.
6
sin
5
x
cos
x
D.
6
cos
5...
Đọc tiếp
Đạo hàm của hàm số y = cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây?
A. - 6 cos 5 x sin x
B. 6 cos 5 x sin x
C. 6 sin 5 x cos x
D. 6 cos 5 x
Cho phương trình: 4(sin4x + cos4x ) – 8(sin6x + cos6x) - 4sin24x m trong đó m là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của m là:
Đọc tiếp
Cho phương trình: 4(sin4x + cos4x ) – 8(sin6x + cos6x) - 4sin24x = m trong đó m là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của m là:
![]()
![]()
![]()
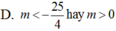
Tìm nhiệm x thuộc (0;pi/2) của phương trình cos9x+cos6x+6cos5x=3
Giải phương trình √3 sin3x – cos3x = √2.
giải các phương trình sau :1. sin( x+pi/4)2/32.cos2x-5sinx-303.cos3xsin2x4.cos3x-sqrt{ }3 với -pi/2x05.4sin^4x + 12cos^2x76.cot(x-1)(cos2x)/(1+tanx) + sin^2x - 1/2sin2x7.sin^23x-cos^24xsin^25x-cos^26x
Đọc tiếp
giải các phương trình sau :
1. sin( x+\(\pi\)/4)=2/3
2.cos2x-5sinx-3=0
3.cos3x=sin2x
4.cos3x=-\(\sqrt{ }\)3 với -\(\pi\)/2<x<0
5.4sin\(^4\)x + 12cos\(^2\)x=7
6.cot(x-1)=(cos2x)/(1+tanx) + sin\(^2\)x - 1/2sin2x
7.sin\(^2\)3x-cos\(^2\)4x=sin\(^2\)5x-cos\(^2\)6x




