Xét u = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có
![]()
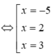
Vậy
Khi đó
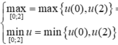
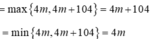
![]()
⇔ - 26 ≤ m ≤ 0
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
Xét u = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có
![]()
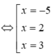
Vậy
Khi đó
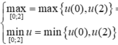
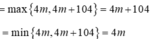
![]()
⇔ - 26 ≤ m ≤ 0
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 3
C. 4
D. 5
Cho hàm số y = x 4 + a x + a x + 1 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn 1 ; 2 . Có bao nhiêu giá trị nguyên của a để M ≥ 2 m .
A. 15
B. 14
C. 17
D. 16
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = x - 6 x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b+ c
A. S = 4
B. S = -2
C. S =-22
D. S = 5
Có bao nhiêu số nguyên m để hàm số y = x 8 + m - 3 x 5 - m 2 - 9 x 4 + 1 đạt giá trị nhỏ nhất tại điểm x = 0.
A. Vô số.
B. 7.
C. 5.
D. 6.
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là các giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên đoạn [ 0;2] Có bao nhiêu số nguyên a thuộc đoạn − 3 ; 3 sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Tìm m để giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn - 2 ; 1 đạt giá trị nhỏ nhất. Giá trị của m là
A. 5
B. 4
C. 1
D. 3
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên 0 ; 2 . Có bao nhiêu số nguyên a thuộc − 4 ; 4 sao cho M ≤ 2 m
A. 7.
B. 5.
C. 6.
D. 4.
Gọi M là giá trị lớn nhất của hàm số y = x 3 - 3 x 2 + x + m xét trên đoạn [2;4], m 0 là giá trị của tham số m để M đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng.
A. 1 < m 0 < 5
B. - 7 < m 0 < - 5
C. - 4 < m 0 < 0
D. m 0 < - 8