Chọn B
Ta có: 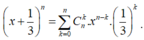
Cho x = 1, ta có:
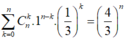
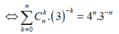
![]()
![]()
Mà ![]()
![]()
Suy ra: ![]()
![]()
![]()
Mà ![]()
Vậy có 1002 số nguyên dương n nghiệm đúng bất phương trình.
Chọn B
Ta có: 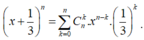
Cho x = 1, ta có:
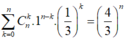
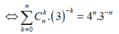
![]()
![]()
Mà ![]()
![]()
Suy ra: ![]()
![]()
![]()
Mà ![]()
Vậy có 1002 số nguyên dương n nghiệm đúng bất phương trình.
Chứng minh rằng:
a) Số các nghiệm tự nhiên của phương trình \(x_1+x_2+...+x_m=n\left(n,m\in N\cdot\right)\) là \(C^n_{m+n-1}\).
b) Số các nghiệm nguyên dương của phương trình \(x_1+x_2+...+x_m=n\left(m\le n;m,n\in N\cdot\right)\) là \(C^{m-1}_{n-1}\).
Em có tìm một số lời giải cho bài toán này nhưng vẫn không hiểu lắm, mong ai đó có lời giải chi tiết và dễ hiểu :)
Cho hàm số f(n)= a n + 1 + b n + 2 + c n + 3 ( n ∈ N * ) với a, b, c là hằng số thỏa mãn a+b+c=0. Khẳng định nào sau đây đúng?
A. lim x → + ∞ f ( n ) = - 1
B. lim x → + ∞ f ( n ) = 1
C. lim x → + ∞ f ( n ) = 0
D. lim x → + ∞ f ( n ) = 2
1/ Giải phương trình sau:
\(tan^2\left(x+\dfrac{\pi}{3}\right)+\left(\sqrt{3}-1\right)tan\left(x+\dfrac{\pi}{3}\right)-\sqrt{3}=0\)
2/ Tìm hệ số của số hạng chứa \(x^{26}\) trong khai triển \(\left(\dfrac{1}{x^4}+x^7\right)^n\) . Biết \(C^2_{n+2}-4C^n_{n+1}=2\left(n+1\right)\) (n ∈ N* ; x > 0)
1) biết các nghiệm của phương trình \(cos2x=-\dfrac{1}{2}\) có dạng \(x=\dfrac{\pi}{m}+k\pi,k\in Z\) với m,n là các số nguyên dương. Khi đó m+n bằng
2) cho \(x=\dfrac{\pi}{3}+k2\pi\left(k\in Z\right)\) là nghiệm của phương trình
3) cho \(x=\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\) là nghiệm của phương trình
Câu 1. Cho tập A = {a;b;c;d;e}. Số tập con của A là:
A. 28 B. 30 C. 32 D. 34
Câu 2. Nghiệm của phương trình ![]() , x
, x ![]() N là:
N là:
A. 8 B. 14 C. 16 D. Vô nghiệm
Câu 3. Hệ só của x6 trong phép khai triển (1 – x2)4 bằng công thức Newton là:
A. ![]() B.
B. ![]() C.
C. ![]() D Một số khác
D Một số khác
Câu 4. Số hạng có chứa y6 trong phép khai triển (x – 2y2)4 là:
A. ![]() B.
B. ![]() C.
C. ![]() D. Một số khác
D. Một số khác
Câu 5. Có 4 trai, 3 gái bầu một ban đại diện ba người. Hỏi có bao nhiêu ban đại diện có ít nhất 2 trai?
A. 18 B. 22 C. 35 D. Một số khác
Câu 6. Giải phương trình: ![]()
A. x = 4 B. x = 6 C. x = 5 D. Một số khác
Câu 7. Nếu ![]() = 220 thì n bằng:
= 220 thì n bằng:
A. 11 B.12 C.13 D.15
Giùm trả lời ạ xin cảm ơn
Cho dãy số ( u n ) xác định bởi u 1 = 0 và u n + 1 = u n + 4 n + 3 , ∀ n ⩾ 2 . Biết :
l i m u n + u 4 n + u 4 2 n + . . . + u 4 2018 n u n + u 2 n + u 2 2 n + . . . + 2 2018 n = a 2019 + b c với a,b,c là các số nguyên dương và b<2019. Tính giá trị S=a+b-c
A.S= -1
B.S=0
C.S=2017
D.S=2018
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2n-1\)
b) \(u_n=3-2n\)
c) \(u_n=\dfrac{n+2}{n}\)
d) \(u_n=\dfrac{2}{n}\)
e) \(u_n=3^n\)
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
Xét tính tăng - giảm của dãy số (un) với
a) un=\(\dfrac{3^n}{2^{n+1}}\)
b) un=\(\dfrac{3^n}{n^2}\)
c) un=\(\sqrt{n}-\sqrt{n-1}\)