Bài 1:
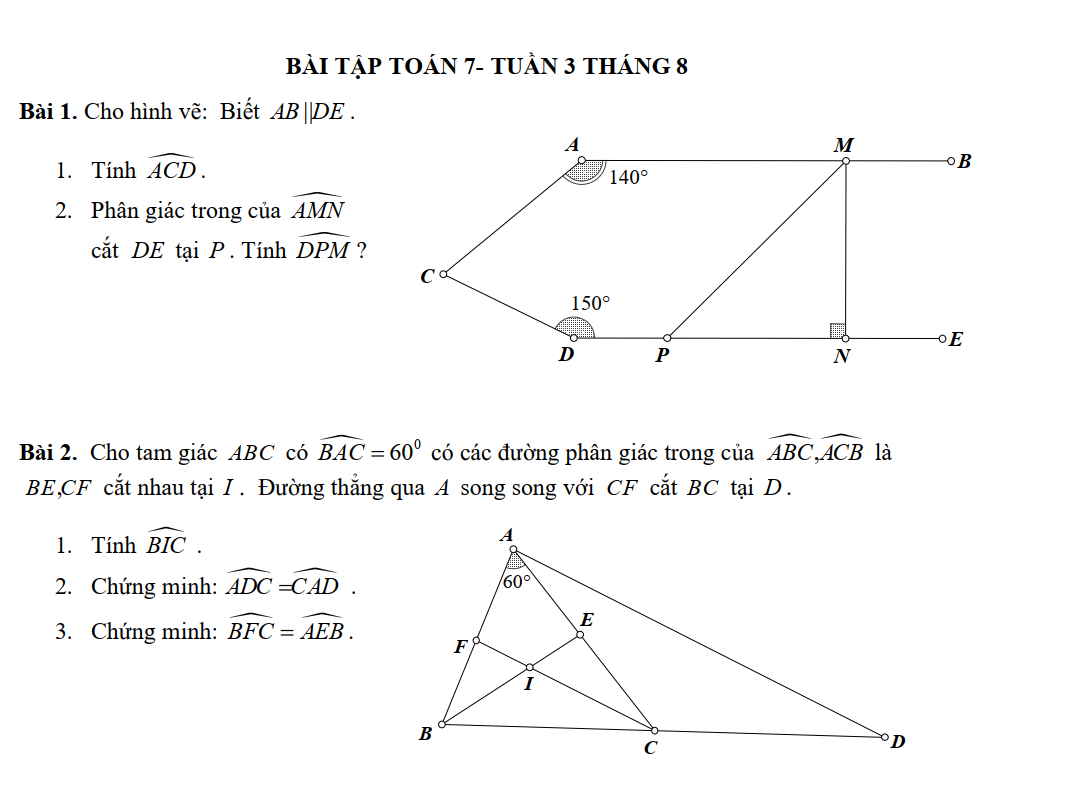
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
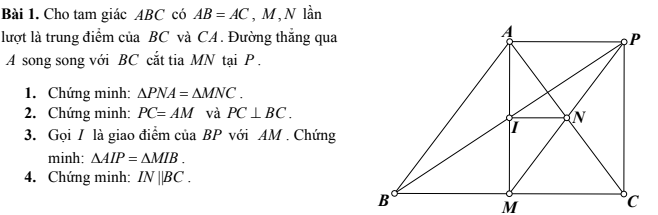
Xét tam giác BIC có:
a)\(\widehat{BIC}=180^0-\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-\left(\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}\right)=180^0-\dfrac{180^0-\widehat{BAC}}{2}=180^0-\dfrac{180^0-60^0}{2}=120^0\)
b) Ta có: FC//AD(gt)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{FCB}=\widehat{ADC}\\\widehat{CAD}=\widehat{ACF}\end{matrix}\right.\)
Mà \(\widehat{FCB}=\widehat{ACF}\)(CF là tia phân giác \(\widehat{ACB}\))
\(\Rightarrow\widehat{ADC}=\widehat{CAD}\)
c) Xét tam giác BFI có:
\(\widehat{BFC}+\widehat{ABI}=\widehat{BIC}=120^0\left(1\right)\)(tính chất góc ngoài tam giác)
Xét tam giác ABE có:
\(\widehat{BAC}+\widehat{AEB}+\widehat{ABI}=180^0\)(tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{AEB}+\widehat{ABI}=180^0-\widehat{BAC}=180^0-60^0=120^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow\widehat{BFC}=\widehat{AEB}\)
Bài 2:
2: Ta có: \(\widehat{ADC}=\widehat{FCB}\)
\(\widehat{CAD}=\widehat{ACF}\)
mà \(\widehat{FCB}=\widehat{ACF}\)
nên \(\widehat{ADC}=\widehat{CAD}\)