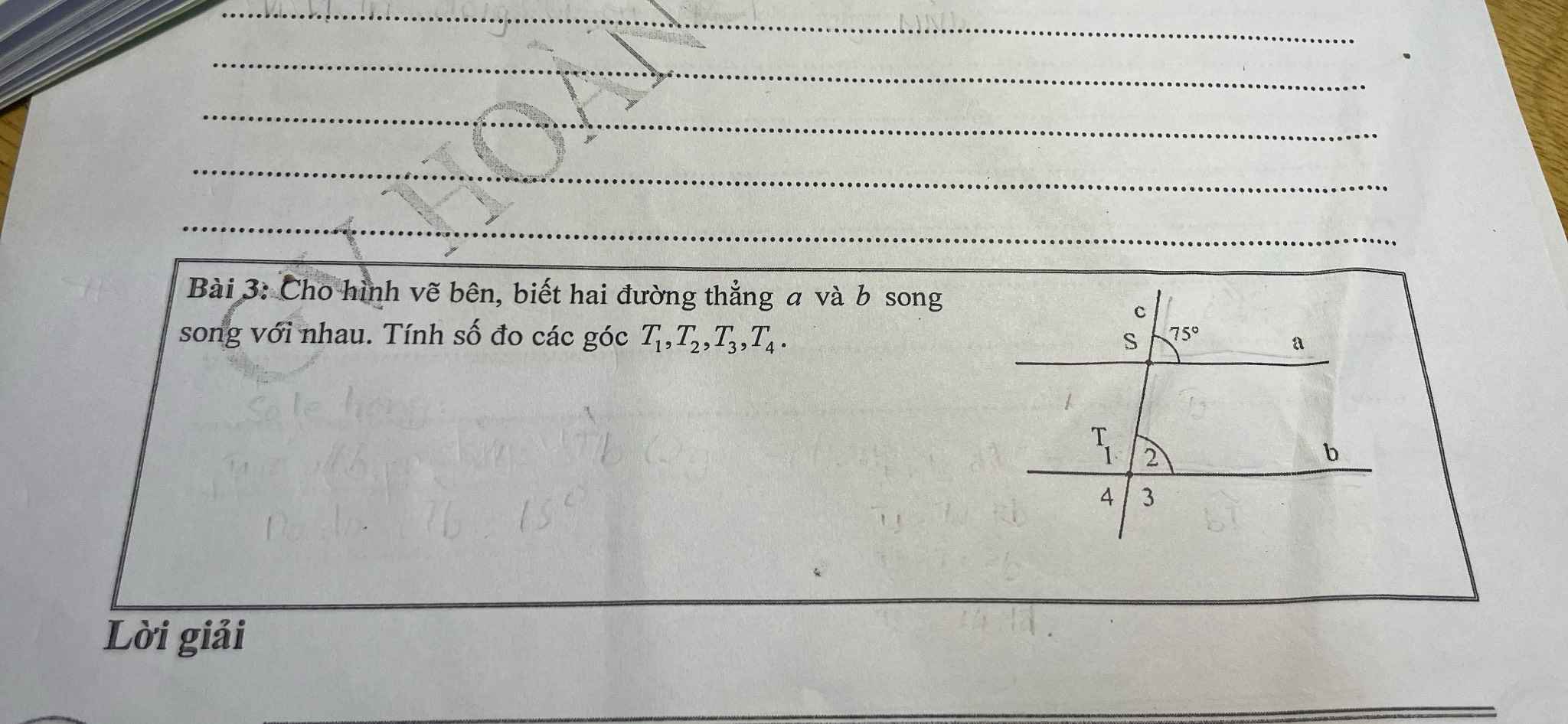a//b
=>\(\widehat{T_2}=\widehat{aSc}\)(hai góc đồng vị)
=>\(\widehat{T_2}=75^0\)
Ta có: \(\widehat{T_2}+\widehat{T_1}=180^0\)(hai góc kề bù)
=>\(\widehat{T_1}+75^0=180^0\)
=>\(\widehat{T_1}=180^0-75^0=105^0\)
Ta có: \(\widehat{T_4}=\widehat{T_2}\)(hai góc đối đỉnh)
mà \(\widehat{T_2}=75^0\)
nên \(\widehat{T_4}=75^0\)
Ta có: \(\widehat{T_3}=\widehat{T_1}\)(hai góc đối đỉnh)
mà \(\widehat{T_1}=105^0\)
nên \(\widehat{T_3}=105^0\)
Theo đè bài ta có `a` // `b`
`=> \(\widehat{cSa}=\widehat{T2}=75^0\)(2 góc đòng vị)
Có:\(\widehat{T2}=\widehat{T4}=75^0\)\(\)(2 góc đối đỉnh)
Lại có :\(\widehat{T2}+\widehat{T1}=180^0\)(2 góc kề bù)
`=> 75^0 + `\(\widehat{T1}\)=180^0`
`=> `\(\widehat{T1}=105^0\)
Mà \(\widehat{T1}=\widehat{T3}\)(đối đỉnh).
`=> `\(\widehat{T3}=105^0\)