Có \(\sin a-\cos a=-\sqrt{2}\left(-\sin a.\sin\dfrac{\pi}{4}+\cos a.\cos\dfrac{\pi}{4}\right)\)
\(=-\sqrt{2}\cos\left(a+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left(\sin a-\cos a\right)^2=2.\cos^2\left(a+\dfrac{\pi}{4}\right)\)
Có \(\sin a-\cos a=-\sqrt{2}\left(-\sin a.\sin\dfrac{\pi}{4}+\cos a.\cos\dfrac{\pi}{4}\right)\)
\(=-\sqrt{2}\cos\left(a+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left(\sin a-\cos a\right)^2=2.\cos^2\left(a+\dfrac{\pi}{4}\right)\)
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Tính cos \(\left(a-\dfrac{\pi}{6}\right)\) biết sina = \(\dfrac{1}{3}\), \(\dfrac{\pi}{2}< a< \pi\)
giải phương trình
a) \(sin\left(x-\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
b) \(cos\left(x+\dfrac{\pi}{4}\right)=cos\dfrac{3\pi}{4}\)
c) \(tan2x=tan\left(x+\dfrac{\pi}{3}\right)\)
d) \(cot2x=-\dfrac{\sqrt{3}}{3}\)
Phương trình \(\left(\sqrt{3}-1\right)sinx-\left(\sqrt{3}+1\right)cosx+\sqrt{3}-1=0\)có các nghiệm là :
A.\(\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
B.\(\left[{}\begin{matrix}x=-\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
C.\(\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{\pi}{9}+k2\pi\end{matrix}\right.\)
D.\(\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k2\pi\\x=\dfrac{\pi}{12}+k2\pi\end{matrix}\right.\)
Giải một trong 4 đáp án trên hộ em ạ em cảm ơn
Biết rằng sina,sinacosa,cosa theo thứ tự lập thành một cấp số cộng. Tính S = sina+cosa
A. 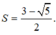
B. 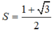
C. 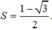
D. 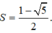
tìm các giá trị lượng giác còn lại
a) \(tanx=\dfrac{3}{2},\pi< x< \dfrac{3\pi}{2}\)
b) \(tanx=\dfrac{\sqrt{3}}{3},0< x< 90\)
c) \(cotx=-\dfrac{1}{\sqrt{3}},\dfrac{3\pi}{2}< x< 2\pi\)
giải phương trình
a) \(sinx=\dfrac{4}{3}\)
b) \(sin2x=-\dfrac{1}{2}\)
c) \(sin\left(x-\dfrac{\pi}{7}\right)\) = \(sin\dfrac{2\pi}{7}\)
d) \(2sin\left(x+\dfrac{\pi}{4}\right)=-\sqrt{3}\)
1) cho góc x thỏa mãn \(cosx=-\dfrac{4}{5}\) và \(\pi< x< \dfrac{3\pi}{2}\) tính \(P=tan\left(x-\dfrac{\pi}{4}\right)\)
2) giải phương trình \(2cosx-\sqrt{2}=0\)
3) phương trình lượng giác \(cos3x=cos\dfrac{\pi}{15}\) có nghiệm là
tìm các giá trị lượng giác còn lại
a) \(tanx=\sqrt{3},0< x< \dfrac{\pi}{2}\)
b) \(cotx=-1,\dfrac{3\pi}{2}< x< 2\pi\)