a) Ta có:\(90^o< \alpha< 180^o\)
\(\Rightarrow\cos\alpha< 0,\tan\alpha< 0,\cot\alpha< 0\)
Do đó:
\(\left\{{}\begin{matrix}\cos\alpha=\sqrt{1-\sin^2}=-\dfrac{4}{5}\\\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=-\dfrac{3}{4}\\\cot\alpha=\dfrac{1}{\tan\alpha}=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có:\(90^o< \alpha< 180^o\)
\(\Rightarrow\cot\alpha< 0,\cos\alpha< 0,\sin\alpha>0\)
Do đó:
\(\left\{{}\begin{matrix}\cot\alpha=\dfrac{1}{\tan\alpha}=-\dfrac{5}{12}\\\cos\alpha=-\sqrt{\dfrac{1}{1+\tan^2}}=-\dfrac{12}{13}\\\sin\alpha=\sqrt{1-\cos^2}=\dfrac{5}{13}\end{matrix}\right.\)
c) Ta có:\(0^o< \alpha< 90^o\)
\(\Rightarrow\tan\alpha>0,\cos\alpha>0,\sin\alpha>0\)
Do đó:
\(\left\{{}\begin{matrix}\tan\alpha=\dfrac{1}{\cot\alpha}=\dfrac{3}{4}\\\sin\alpha=\sqrt{\dfrac{1}{1+\cot^2}}=\dfrac{3}{5}\\\cos\alpha=\sqrt{1-\sin^2}=\dfrac{4}{5}\end{matrix}\right.\)
d) Ta có:\(0^o< \alpha< 90^o\)
\(\Rightarrow\tan\alpha>0,\cot\alpha>0,\sin\alpha>0\)
Do đó:
\(\left\{{}\begin{matrix}\sin\alpha=\sqrt{1-\cos^2\alpha}=\dfrac{\sqrt{5}}{3}\\\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{\sqrt{5}}{2}\\\cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{2}{\sqrt{5}}\end{matrix}\right.\)
Do xài điện thoại không có ký hiệu alpha nên thay bằng chữ a nhé em!
a) Do 90⁰ < a < 180⁰ nên cosa < 0, tân < 0, cota < 0
Ta có:
sin²a + cos²a = 1
cos²a = 1 - sin²a
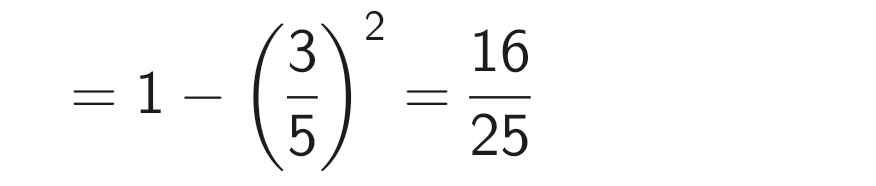
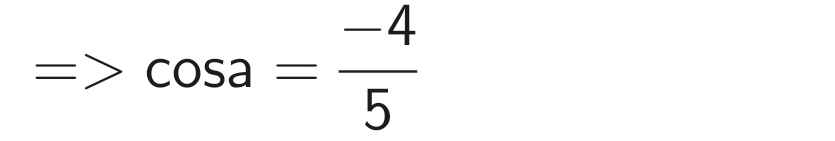
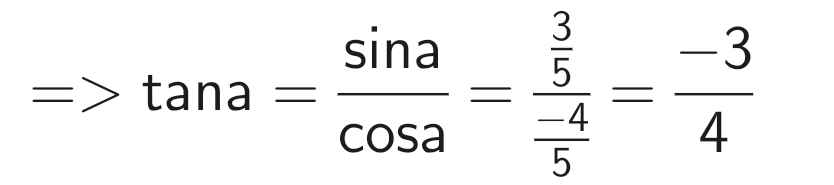
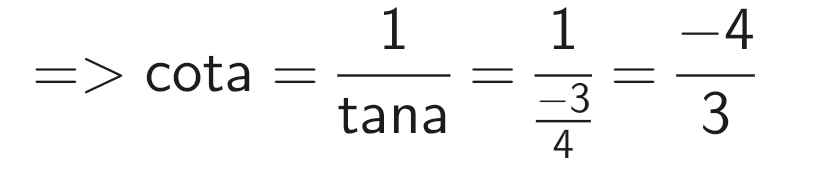
b) Do 90⁰ < a < 180⁰ nên sina > 0, cosa < 0, cota < 0
Ta có:
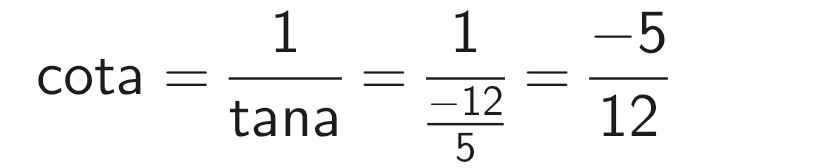
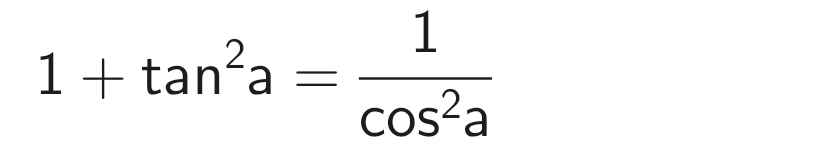
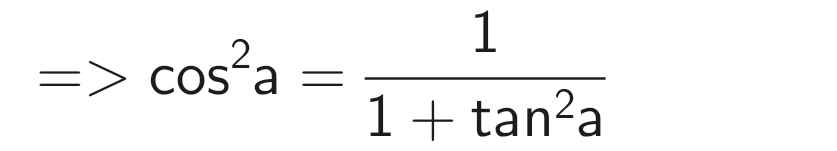
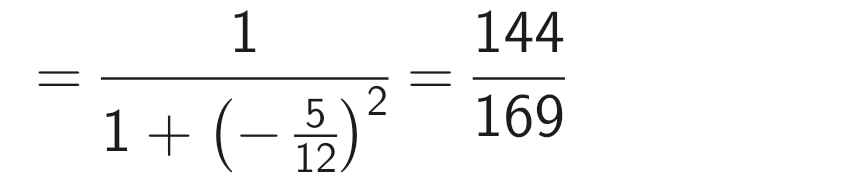
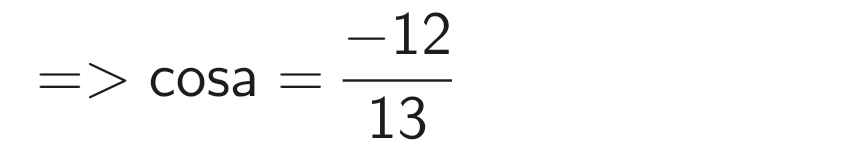
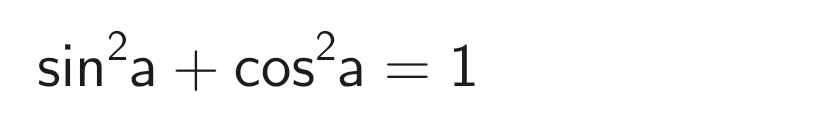
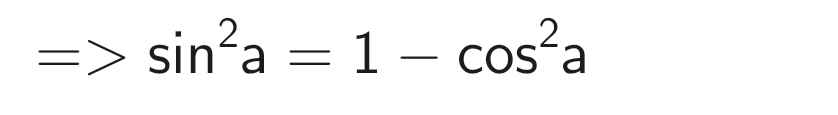
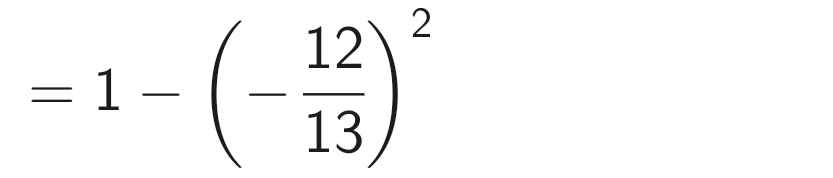

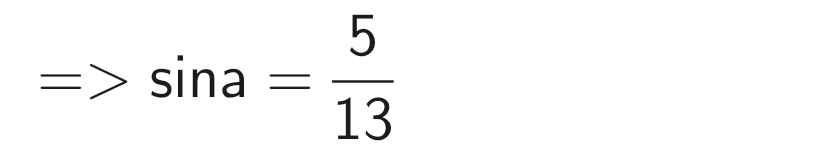

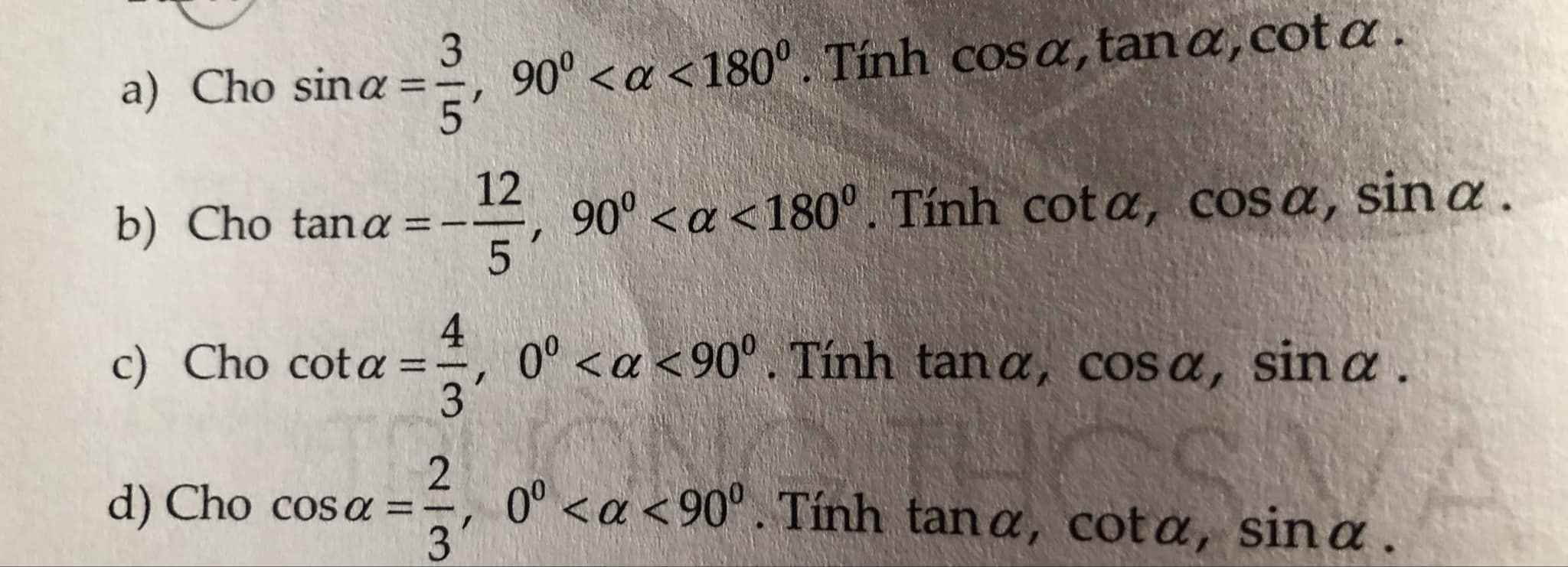 cíu tui cíu tui
cíu tui cíu tui





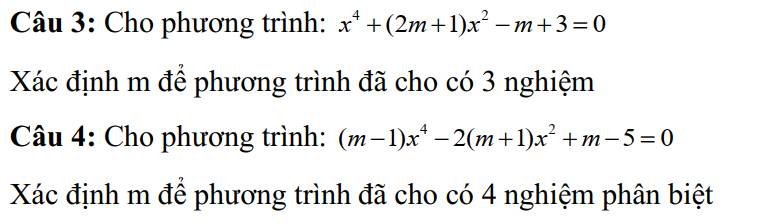 CÍU TUIIII
CÍU TUIIII
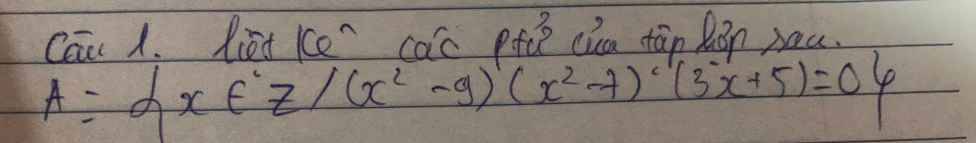 cíu bé vs mn ơi
cíu bé vs mn ơi