Câu 4: \(\left(m-1\right)x^4-2\left(m+1\right)x^2+m-5=0\)(1)
Đặt \(a=x^2\left(a>=0\right)\)
Phương trình (1) sẽ trở thành:
\(\left(m-1\right)\cdot a^2-2\left(m+1\right)a+m-5=0\)(2)
Để phương trình (1) có 4 nghiệm phân biệt thì phương trình (2) có 2 nghiệm dương phân biệt
=>\(\left\{{}\begin{matrix}m-1\ne0\\\left[-2\left(m+1\right)\right]^2-4\left(m-1\right)\left(m-5\right)>0\\\dfrac{2\left(m+1\right)}{m-1}>0\\\dfrac{m-5}{m-1}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\4m^2+8m+4-4m^2+24m-20>0\\\dfrac{m+1}{m-1}>0\\\left[{}\begin{matrix}m>5\\m< 1\end{matrix}\right.\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\32m-16>0\\\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\\left[{}\begin{matrix}m>5\\m< 1\end{matrix}\right.\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m>\dfrac{1}{2}\\\left[{}\begin{matrix}m>5\\m< -1\end{matrix}\right.\\\end{matrix}\right.\)
=>\(m>5\)
3.
Đặt \(x^2=t\ge0\) \(\Rightarrow x=\pm\sqrt{t}\)
- Nếu \(t>0\) sẽ cho 2 nghiệm x phân biệt
- Nếu \(t=0\) cho 1 nghiệm \(x=0\)
- Nếu \(t< 0\Rightarrow\) ko tồn tại nghiệm x tương ứng
Phương trình trở thành:
\(t^2+\left(2m+1\right)t-m+3=0\) (1)
Từ trên ta thấy pt đã cho có 3 nghiệm khi và chỉ khi (1) có 2 nghiệm pb sao cho 1 nghiệm dương và 1 nghiệm bằng 0
Do pt có 1 nghiệm bằng 0 \(\Rightarrow-m+3=0\Rightarrow m=3\)
Khi đó: \(t^2+7t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=-7< 0\left(ktm\right)\end{matrix}\right.\)
Vậy không tồn tại m thỏa mãn yêu cầu

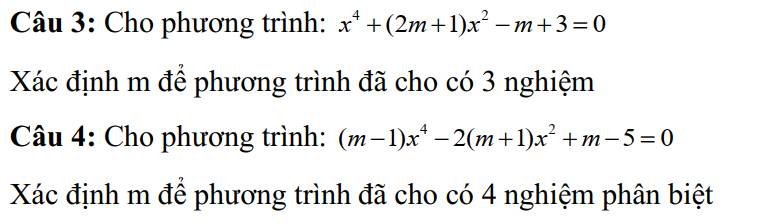 CÍU TUIIII
CÍU TUIIII





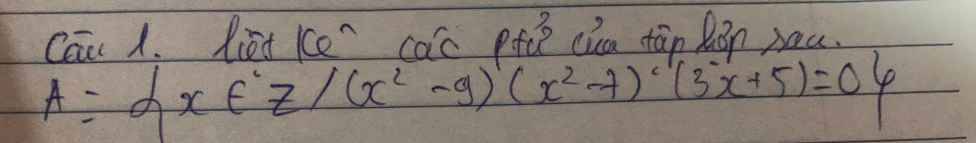 cíu bé vs mn ơi
cíu bé vs mn ơi






