Ta có:
x + 2 2 x - 4 = 2 + x - 2 2
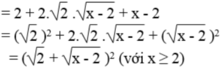
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Ta có:
x + 2 2 x - 4 = 2 + x - 2 2
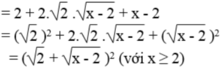
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Chứng minh: \(\frac{2^x}{4^x+1}+\frac{4^x}{2^x+1}+\frac{2^x}{2^x+4^x}=\frac{3}{2}\)
Cho 0<x<2. Chứng minh rằng:
\(\dfrac{4-\sqrt{4-x^2}}{\sqrt{\left(2+x\right)^3}+\sqrt{\left(2-x\right)^3}}\) + \(\dfrac{4+\sqrt{4-x^2}}{\sqrt{\left(2+x\right)^3}-\sqrt{\left(2-x\right)^3}}\) = \(\dfrac{\sqrt{2+x}}{x}\)
Chứng minh:
x^3/y^2 + 9y^2/(x+2y) >= 4 ( biết x^2+y^2 =2)
Chứng minh rằng với x,y khác 0 ta có
x^2/y^2+y^2/x^2+4>=3(x/y+y/x)
cho x,y là 2 số thực dương. chứng minh rằng: \(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}-\dfrac{3x}{y}-\dfrac{3y}{x}+4\ge0\)
a,Tính giá trị của A khi x=4
b,Tính giá trị của A khi x=(2-căn 3)^2
c,Tính giá trị của A khi x=7-2 căn 3
d,Tìm x để A=2
e,TÌm x để A>1
chứng minh 2√x - ( 2 - √x) =4
chứng minh p=\(\left(\dfrac{\sqrt[4]{x^2}-\sqrt[4]{x}}{1-\sqrt[4]{x}}+\dfrac{1+\sqrt{x}}{\sqrt[4]{x}}\right)^2-\dfrac{\sqrt{1+\dfrac{2}{\sqrt{x}}+\dfrac{1}{x}}}{1+\sqrt{x}}\)(x>0)không phụ thuộc vào x
Cho P=\(P=\sqrt{x^2+\sqrt[3]{x^4y^2}}+\sqrt{y^2+\sqrt[3]{x^2y^4}}\). Chứng minh rằng: \(\sqrt[3]{P^2}=\sqrt[3]{x^2}+\sqrt[3]{y^2}\)