
Từ đó
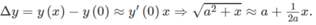
Áp dụng:
a) 12,08;
b) 5,83;
c) 10,95.

Từ đó
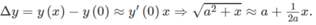
Áp dụng:
a) 12,08;
b) 5,83;
c) 10,95.
1. Cho đa thức \(f\left(x\right)=x^3-3x^2+9x+1964\). Chứng minh rằng tồn tại số nguyên \(a\) sao cho \(f\left(a\right)⋮3^{2014}\)
2. Chứng minh rằng với mọi \(a\inℤ\), phương trình \(x^4-2007x^3+\left(2006+a\right)x^2-2005x+a=0\) không thể có 2 nghiệm nguyên phân biệt.
3. Tìm tất cả các số nguyên dương \(n\) sao cho \(2^n-1|3^n-1\)
Chứng minh rằng với mọi số thực a, b, c phương trình: ( x – a ) . ( x - b ) + ( x - b ) . ( x - c ) + ( x – c ) . ( x - a ) = 0 có ít nhất một nghiệm.
Chứng minh rằng các phương trình sau luôn có nghiệm: a)x^5 - 3x+3=0 b)x^5+x-1=0 c)x^4+x^3-3x^2+x+1=0
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Chứng minh các tính chất a), b) và c).
a) P ∅ = 0 , P Ω = 1 .
b) 0 ≤ P A ≤ 1 , với mọi biến cố A.
c) Nếu A và B xung khắc, thì
P A ∪ B = P A + P B (công thức cộng xác suất).
Cho ba số phân biệt a,b,c \(\in\) R. Chứng minh rằng phương trình:
\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\) luôn có hai nghiệm phân biệt
Cho hàm số y = f(x) xác định trên khoảng (a; +∞)
Chứng minh rằng nếu lim x → + ∞ f ( x ) = - ∞ thì luôn tồn tại ít nhất một số c thuộc (a; +∞) sao cho f(c) < 0
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
A. f x + x 2 = 0
B. f x + a = 0
C. f x - x = 0
D. f x + x = 0