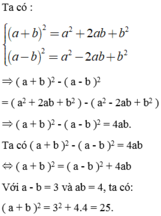Các câu hỏi tương tự
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a + b = 6 và ab = 8
Chứng minh
a) ( a - b )^2 = ( a + b ) - 4ab. Tính ( a - b )^2009 biết a + b = -3 và ab = 4
b) a^3 + b^3 = ( a + b )^3 - 3ab(a + b ). Tính a^3 + b^3 = biết ab = 5 và a + b = -8
c) a^3 - b^3 = ( a - b )^3 + 3ab( a -b ). Tính a^3 - b^3 biết ab = -4 và a - b = 6
d) x^2 - 2xy + y^2 + 1 > 0 với mọi x và y
e) Tính x + y biết x^3 + y^3 = 91 và x^2 - xy + y^2 = 13
a)Chứng minh rằng nếu a^4 +b^4 +c^4 +d^4 =4abcd và a,b,c,d là các số dương thì a =b=c=d
b)Chứng minh rằng nếu m= a+ b +c thì (am+ bc )(bm+ac)(cm+ab)= (a+b)^2 (a+c )^2 (b+c)^2
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
chứng minh rằng : (a+b)^2 = (a-b)^2 + 4ab
áp dụng tính (a+b)^2 biết a-b=10 và ab=0
Chứng minh rằng:
(a + b)2 = (a – b)2 + 4ab
(a – b)2 = (a + b)2 – 4ab
Áp dụng:
a) Tính (a – b)2, biết a + b = 7 và a.b = 12.
b) Tính (a + b)2, biết a – b = 20 và a.b = 3.
Chứng minh : (a-b)^2 = (a+b)^2 -4ab . Tính (a-b)^2009 biết a+b=-3 và a.b=4
cho a,b >0 và a+b ≤ 1. chứng minh rằng ab+1/a^2+1/b^2 ≥ 33/4
chứng minh \(a^4+b^4+4a^2b^2 ≥3(a^3b+ab^3)\) biết rằng a,b > 0