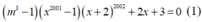
- Đặt:
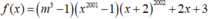
- Tập xác định của hàm số f(x) là D = R.
- Vì f(x) là hàm đa thức nên f(x) liên tục trên R. Ta có:
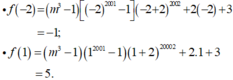
- Vì f(-2).f(1) = -5 < 0 với mọi m.
- Suy ra: f(x) = 0 luôn có ít nhất 1 nghiệm x 0 ∈ ( - 2 ; 1 ) với mọi m.
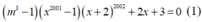
- Đặt:
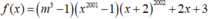
- Tập xác định của hàm số f(x) là D = R.
- Vì f(x) là hàm đa thức nên f(x) liên tục trên R. Ta có:
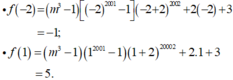
- Vì f(-2).f(1) = -5 < 0 với mọi m.
- Suy ra: f(x) = 0 luôn có ít nhất 1 nghiệm x 0 ∈ ( - 2 ; 1 ) với mọi m.
Chứng minh phương trình sau có nghiệm với mọi m: m ( x - 1 ) ( x + 2 ) + 2 x + 1 = 0 ( 1 )
Chứng minh rằng phương trình sau luôn có nghiệm với mọi tham số $m$:
$m{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{3}}+\left( x+2 \right)\left( x-3 \right)=0$.
Chứng minh phương trình sau có ít nhất 2 nghiệm phân biệt Với mọi m thuộc R. đặt f(x)=X^4+(m-2)x^3+x^3+(3m+1)x-4m-2016=0
Chứng minh các phương trình sau luôn có nghiệm với mọi giá trị của tham số m ( 1 − m 2 ) x + 1 3 + x 2 – x – 3 = 0
Chứng minh rằng với mọi tham số thực m, phương trình x6 - 65 + m.\(\sqrt[3]{2-x}\) = m(1-\(\sqrt{x-1}\) ) luôn có nghiệm.
Chứng minh phương trình \(\left(m^2+m+1\right)x^4+2x-2=0\)0 có nghiệm với mọi m
Chứng mỉnh rằng phương trình −x3+(1−m)2 x2+4x +1 =0 có 3 nghiệm phân biệt với mọi m
a. CMR: Với mọi tham số m phương trình \(\left(1-m^2\right)x^3-6x=1\) luôn có nghiệm
b. CMR PT \(x^3+2x=4+3\sqrt{3-2x}\) có đúng 1 nghiệm
c. CMR PT \(\left(m-1\right)\left(x-2\right)^2\left(x-3\right)^3+2x-5=0\) có nghiệm với mọi m
\(\left(1+m^2\right)\left(x-1\right)^3+x^2-2=0\)
Chứng minh pt trên có ít nhất 1 nghiệm dương với mọi tham số m