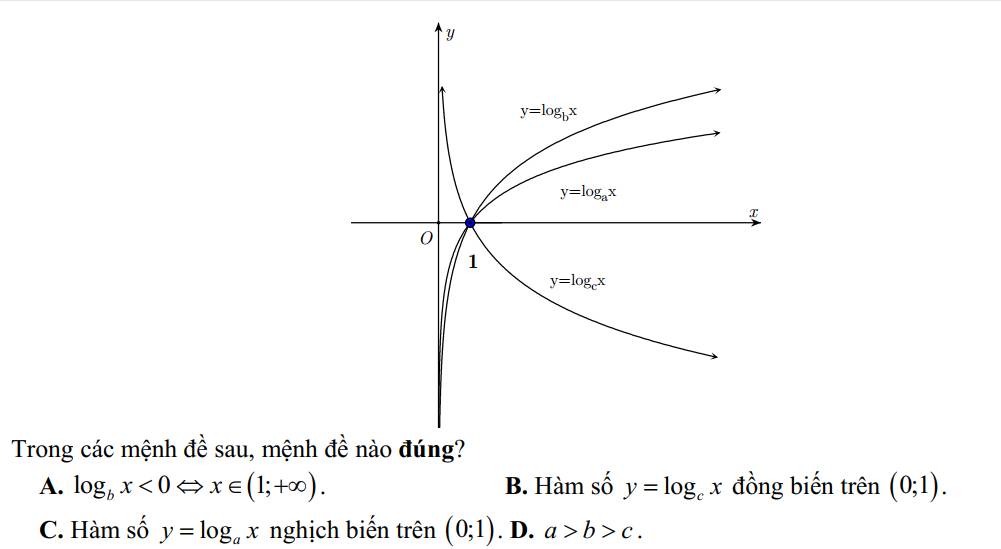
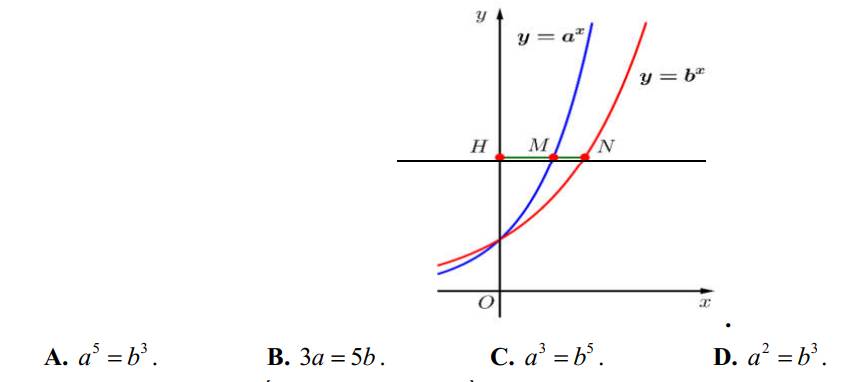
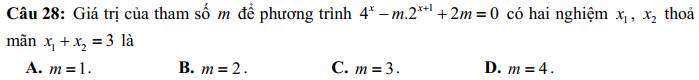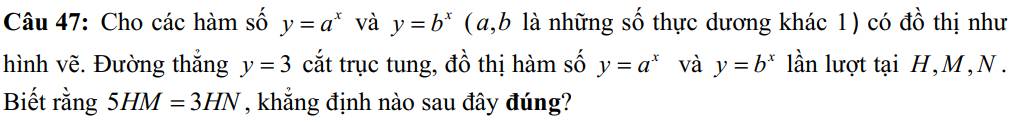28D
HD: ĐK: \(m\left(m-2\right)\ge0\)
\(2^{x_1}.2^{x_2}=2m\). Mà theo gt thì \(x_1+x_2=3\) nên \(2^3=2m\Leftrightarrow m=4\left(tm\right)\)
37B
HD: \(a^xb^{x^2-2}=1\Leftrightarrow a^x=b^{2-x^2}\)
Do \(a,b>1\) nên \(xlog_ba=2-x^2\)\(\Leftrightarrow log_ba=\dfrac{2-x^2}{x}\)
Do đó
\(\dfrac{2-x_1^2}{x_1}=\dfrac{2-x_2^2}{x_2}>0\)
Đặt \(x_1+x_2=t\) thì ta có:
\(\left\{{}\begin{matrix}x_1x_2=-2\\t< 0\end{matrix}\right.\)
Do đó: \(T=\dfrac{4}{t^2}-5t=\dfrac{4}{t^2}+\left(-\dfrac{5t}{2}\right)+\left(-\dfrac{5t}{2}\right)\ge3\sqrt[3]{\dfrac{4}{t^2}.\left(-\dfrac{5t}{2}\right)^2}=3\sqrt[3]{25}\)
Đẳng thức xảy ra\(\Leftrightarrow t=-\dfrac{2}{\sqrt[3]{5}}\Rightarrow\left\{{}\begin{matrix}x_1=...\\x_2=...\end{matrix}\right.\)
38. Không có đáp án đúng
HD: ĐK:\(\left[{}\begin{matrix}m\ge-6+18\sqrt{3}\\m\le-6-18\sqrt{3}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3^{x_1}.3^{x_2}=243\left(1\right)\\3^{x_1}+3^{x_2}=m+6\left(2\right)\end{matrix}\right.\)
Từ (1)\(\Rightarrow x_1+x_2=5\)
Kết hợp với gt, ta có:
\(x_1.x_2=7\)\(\Rightarrow\) Không có x thoả mãn, đề sai
(Đề có thể sửa lại là \(\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_1x_2}=1\), khi đó \(x_1=2;x_2=3;m=30\)
là hợp lý)
39C
HD: Gt \(\Rightarrow3^x-3^{-x}=2cos\left(nx\right)\) (*)
PT đã cho tđ vs:
\(9^x+\dfrac{1}{9^x}=4+2.\left(2cos^2\left(nx\right)-1\right)=4cos^2\left(nx\right)+2\)
\(\Leftrightarrow\left(3^x-3^{-x}\right)^2=4cos^2\left(nx\right)\)\(\Leftrightarrow\left[{}\begin{matrix}3^x-3^{-x}=2cos\left(nx\right)\\3^x-3^{-x}=-2cos\left(nx\right)\end{matrix}\right.\)
Do pt (*) có 2023 nghiệm nên pt đã cho có 2.2023=4046 nghiệm