Các câu hỏi tương tự
Tìm tất cả các số thực x, y để hai số phức
z
1
9
y
2
-
4
-
10
x
i
5
,
z
2
8
y
2
+
10
i
11
là hai số phức liên hợp của nhau. A.
x...
Đọc tiếp
Tìm tất cả các số thực x, y để hai số phức z 1 = 9 y 2 - 4 - 10 x i 5 , z 2 = 8 y 2 + 10 i 11 là hai số phức liên hợp của nhau.
A. x = 2 y = ± 2
B. x = ± 2 y = 2
C. x = - 2 y = ± 2
D. x = - 2 y = 2
Cho số phức
z
x
+
iy
,
x
,
y
∈
ℝ
. Tập hợp các điểm
M
x
;
y
biểu diễn số phức z là phần hình phẳng được tô màu như hình vẽ (tính cả đường viền). Khẳng định nào sau đây đúng? A. Số phức z có môđun nằm trong đoạn
1...
Đọc tiếp
Cho số phức z = x + iy , x , y ∈ ℝ . Tập hợp các điểm M x ; y biểu diễn số phức z là phần hình phẳng được tô màu như hình vẽ (tính cả đường viền). Khẳng định nào sau đây đúng?
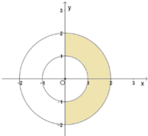
A. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần thực không âm
B. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần ảo không âm
C. Số phức z có môđun nằm trong khoảng 1 ; 2 và phần thực dương
D. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần ảo dương
Gọi M là điểm biểu diễn số phức zx+yi, x,y ∈R, điểm biểu diễn số phức liên hợp của z bằng cách A. lấy đối xứng M qua trục hoành B. lấy đối xứng M qua đường thẳng y x C. lấy đối xứng M qua trục tung D. lấy đối xứng M qua trục tọa độ
Đọc tiếp
Gọi M là điểm biểu diễn số phức z=x+yi, x,y ∈R, điểm biểu diễn số phức liên hợp của z bằng cách
A. lấy đối xứng M qua trục hoành
B. lấy đối xứng M qua đường thẳng y =x
C. lấy đối xứng M qua trục tung
D. lấy đối xứng M qua trục tọa độ
Gọi M là điểm biểu diễn số phức
z
x
+
yi
,
x
,
y
∈
ℝ
điểm biểu diễn số phức liên hợp của z bằng cách A. Lấy đối xứng M qua trục tọa độ B. Lấy đối xứng M qua trục hoành C. Lấy đối xứng M qua đường thẳng yx D. Lấy đối xứng M qua trục tung
Đọc tiếp
Gọi M là điểm biểu diễn số phức z = x + yi , x , y ∈ ℝ điểm biểu diễn số phức liên hợp của z bằng cách
A. Lấy đối xứng M qua trục tọa độ
B. Lấy đối xứng M qua trục hoành
C. Lấy đối xứng M qua đường thẳng y=x
D. Lấy đối xứng M qua trục tung
Cho hai số phức z,z’. Cặp số nào sau đây không là hai số phức liên hợp của nhau?
A
.
z
+
z
v
à
z
+
z
B
.
z
z
v
à
z
z
C
.
z
-
z...
Đọc tiếp
Cho hai số phức z,z’. Cặp số nào sau đây không là hai số phức liên hợp của nhau?
A . z + z ' v à z + z '
B . z z v à z z '
C . z - z v à z - z '
D . z z ' v à z z '
Xét các số phức
z
x
+
y
i
x
,
y
∈
ℝ
có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
C
:
x
-
1
2
+
y
-...
Đọc tiếp
Xét các số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình C : x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
A. Đường thẳng
B. Đoạn thẳng.
C. Điểm
D. Đường tròn.
Xét các số phức
z
x
+
y
i
x
,
y
∈
ℝ
có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
(
C
)
:
x
-
1
2
+
y
-...
Đọc tiếp
Xét các số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình ( C ) : x - 1 2 + y - 2 2 = 4 . Tập hợp các điểm biểu diễn của số phức là w = z + z ¯ + 2 i
A. Đường thẳng
B. Đoạn thẳng
C. Điểm
D. Đường tròn
Cho số phức
z
x
+
y
i
x
,
y
∈
ℝ
. Tập hợp các điểm biểu diễn của số phức z sao cho số phức
z
+
i
z
-
i
là một số thực âm là: A. Các điểm trên trục hoành với -1 x 1 B. Các điểm trên trục tung...
Đọc tiếp
Cho số phức z = x + y i x , y ∈ ℝ . Tập hợp các điểm biểu diễn của số phức z sao cho số phức z + i z - i là một số thực âm là:
A. Các điểm trên trục hoành với -1 < x < 1
B. Các điểm trên trục tung với -1 < y < 1
C. Các điểm trên trục tung với - 1 ≤ y < 1
D. Các điểm trên trục tung với | y ≥ 1 y ≤ - 1
Cho các mệnh đề sau(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm(II) Trên tập hợp các số phức thì số thực âm không có căn bậc hai(III) Môđun của một số phức không phải là một số phức(IV) Môđun của một số phức là một số thực dươngTrong bốn mệnh đề trên có bao nhiêu mệnh đề đúng? A. 2 B. 4 C. 3 D. 1
Đọc tiếp
Cho các mệnh đề sau
(I) Trên tập hợp các số phức thì phương trình bậc hai luôn có nghiệm
(II) Trên tập hợp các số phức thì số thực âm không có căn bậc hai
(III) Môđun của một số phức không phải là một số phức
(IV) Môđun của một số phức là một số thực dương
Trong bốn mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 2
B. 4
C. 3
D. 1