Question

Cho tứ giác XYZT . E , F lần lượt là trung điểm của XY , ZT . Chứng minh : EF ≤ \(\dfrac{XT+YZ}{2}\)    

Mong bạn giúp mình nhanh nhất nhé!

Answer 1

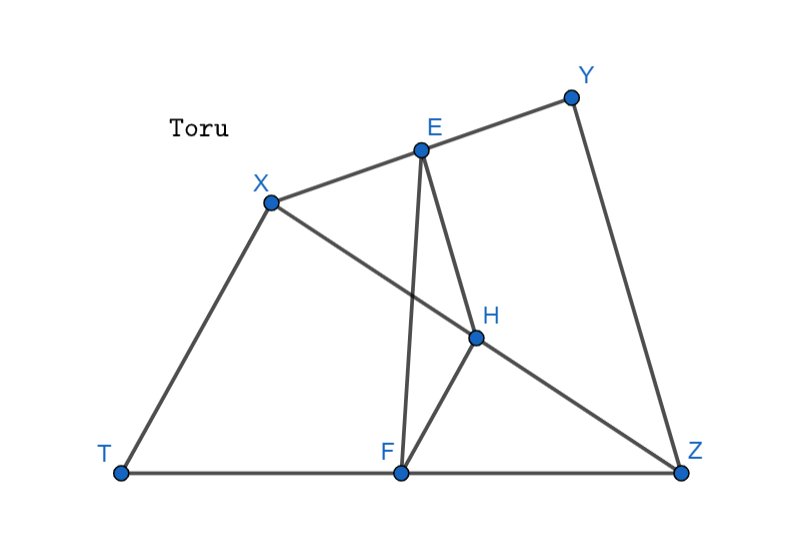
Gọi H là trung điểm của XZ

Xét \(\triangle XZT\) có: \(\left\{{}\begin{matrix}H\text{ là trung điểm của }XZ\\F\text{ là trung điểm của }ZT\end{matrix}\right.\)

\(\Rightarrow HF\) là đường trung bình của \(\triangle XZT\) \(\Rightarrow \begin{cases} HF//XT\\HF=\frac{XT}{2} \end{cases}\) (t/c)

Xét \(\triangle XYZ\) có: \(\left\{{}\begin{matrix}E\text{ là trung điểm của }XY\\H\text{ là trung điểm của }XZ\end{matrix}\right.\)

\(\Rightarrow EH\) là đường trung bình của \(\triangle XYZ\) \(\Rightarrow \begin{cases} EH//YZ\\EH=\frac{YZ}{2}\end{cases}\) (t/c) 

Với ba điểm E, H, F ta có: \(EF\le EH+HF=\dfrac{YZ}{2}+\dfrac{XT}{2}=\dfrac{XT+YZ}{2}\)

Dấu "=" xảy ra khi: E, H, F thẳng hàng

Mà: \(\begin{cases} HF//XT\\ EH//YZ\end{cases} \Rightarrow \begin{cases}EF//XT\\EF//YZ\end{cases}\Rightarrow XT//YZ\)

`=>` Tứ giác XYZT là hình thang (XT//YZ)

#$\mathtt{Toru}$

Answer 2