Đáp án B.
A B → . A C → = A B → . A D → ⇔ A B → A C → − A D → = 0 ⇔ A B → . D C → = 0 ⇔ A B ⊥ D C .
Đáp án B.
A B → . A C → = A B → . A D → ⇔ A B → A C → − A D → = 0 ⇔ A B → . D C → = 0 ⇔ A B ⊥ D C .
Câu 1: Hình thang ABCD (AB // CD) có AC vuông góc BD tại O. Biết AB=3,5 cm; AD=5,2 cm. Gọi M là trung điểm CD. Tính diện tích AMO.
Câu 2: Cho hình thang cân ABCD có đáy nhỏ AB=7cm; BD vuông góc BC. Kẻ BH vuông góc CD(với H thuộc CD). Biết BH=5cm. Tính diện tích ABCD và góc BCD.
Câu 3: Cho hình thang cân ABCD có đáy nhỏ AB=BC= \(\frac{1}{2}\)CD và AC=4cm. Tính góc C và diện tích ABCD.
Câu 4: Cho hình thang cân ABCD có AB//CD, BC=12cm, AC=15cm. Tính góc C và diện tích ABCD.
Câu 5: Cho hình thang vuông ABCD (vuông ở A và B0 có E là trung điểm CD; AE cắt BC tại F. Biết AD=1,5 cm; BC=2,7 cm; AB=2cm. Tính các góc và diện tích của tam giác BEF.
Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc với nhau từng đôi một (như hình vẽ bên dưới). Khẳng định nào sau đây sai?
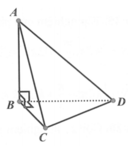
A. Góc giữa AD và (ABC) là góc A D B ^
B. Góc giữa CD và (ABD) là góc C D B ^
C. Góc giữa AC và (BCD) là góc A C B ^
D. Góc giữa AC và (ABD) là góc C A B ^
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B có AB =3, BC =4. S A ⊥ A B C và SA =5. Gọi H là hình chiếu vuông góc của A lên SB và K là trung điểm của SC. Khẳng định nào sau đây đúng?
A. (AHK)//BC
B. A H K ⊥ S B C
C. A H K ⊥ S B
D. A H K ⊥ S A B
Cho tứ diện đều ABCD có cạnh bằng 1. M, N lần lượt là các điểm di động trên các cạnh AB, AC sao cho hai mặt phẳng (DMN), (ABC) vuông góc với nhau. Đặt A M = x , A N = y Đẳng thức nào sau đây đúng?
A. x y ( x + y ) = 3
B. x + y = 3 x y
C. x + y = 3 + x y
D. x y = 3 ( x + y ) .
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có BD vuông góc với AB và CD. Gọi P và Q lần lượt là trung điểm của của các cạnh CD và AB thỏa mãn BD:CD:PQ:AB = 3:4:5:6 . Gọi φ là góc giữa hai đường thẳng AB và CD. Giá trị của cosφ bằng
A. 7/8.
B. 1/2.
C. 11/16.
D. 1/4.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B. H là trực tâm tam giác ABC
C. O A ⊥ B C
D. A H ⊥ O B C
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B.H là trực tâm tam giác ABC
C. O A ⊥ B C
D. A H ⊥ O B C
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B. H là trực tâm tam giác ABC
C. OA ⊥ BC
D. AH ⊥ (OBC)