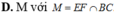Các câu hỏi tương tự
Cho tứ diện S.ABC. Gọi D là điểm trên SA, E là điểm trên SB và F là điểm trên AC (DE và AB không song song). Tìm giao điểm của BC với mặt phẳng (DEF). A. M với
M
D
F
∩
B
C
B. M với
M
D
E
∩
B
C
C. M với
M
N
F
∩
B
C
,
N...
Đọc tiếp
Cho tứ diện S.ABC. Gọi D là điểm trên SA, E là điểm trên SB và F là điểm trên AC (DE và AB không song song). Tìm giao điểm của BC với mặt phẳng (DEF).
A. M với M = D F ∩ B C
B. M với M = D E ∩ B C
C. M với M = N F ∩ B C , N = D E ∩ A B
D. M với M = E F ∩ B C
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng α song song với (SIC). Thiết diện tạo bởi và tứ diện S.ABC là:
A. hình bình hành.
B. tam giác cân tại M.
C. tam giác đều.
D. hình thoi.
Cho hình chóp S.ABC có SASBCACBABa,
S
C
a
3
2
, G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng A. ...
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng
A. 90 0 C
B. 45 0 C
C. 30 0 C
D. 60 0 C
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 1, AC 2; cạnh bên SA vuông góc với đáy và SA 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho
A
M
x
0
x
1
và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng. A. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1 và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
A. 2 3
B. 3 4
C. 1 3
D. 1 2
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng
α
song song với
S
C
I
. Tính chu vi của thiết diện tạo bởi
α
và tứ diện S.ABC tính theo
A
M
a
. A.
a
1
+
3
B....
Đọc tiếp
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng α song song với S C I . Tính chu vi của thiết diện tạo bởi α và tứ diện S.ABC tính theo A M = a .
A. a 1 + 3
B. 2 a 1 + 3
C. 3 a 1 + 3
D.Không tính được
Cho tứ diện S.ABC. Gọi I trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng α song song (SIC). Thiết diện tạo bởi α với tứ diện S.ABC là
A. Hình bình hành
B. Tam giác cân tại M
C. Tam giác đều
D. Hình thoi
Cho tứ diện S.ABC trên cạnh SA và SB lấy điểm M và N sao cho thỏa tỉ lệ
S
M
A
M
1
2
;
S
N
N
B
2
, mặt phẳng đi qua MN và song song với SC chia tứ diện thành hai phần, biết tỉ số thể tích của hai phần ấy là K, vậy K là gi...
Đọc tiếp
Cho tứ diện S.ABC trên cạnh SA và SB lấy điểm M và N sao cho thỏa tỉ lệ S M A M = 1 2 ; S N N B = 2 , mặt phẳng đi qua MN và song song với SC chia tứ diện thành hai phần, biết tỉ số thể tích của hai phần ấy là K, vậy K là giá trị nào?
A. K = 2 3
B. K = 4 9
C. K = 4 5
D. K = 5 9
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho
S
M
M
A
1
2
;
S
N
N
B
2
.
Mặt phẳng
α
đi qua MN và song song với SC chia khối chóp thàng 2 phần. Gọi...
Đọc tiếp
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho S M M A = 1 2 ; S N N B = 2 . Mặt phẳng α đi qua MN và song song với SC chia khối chóp thàng 2 phần. Gọi V 1 là thể tích của khối đa diện chứa A , V 2 là thể tích của khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 4 5
B. V 1 V 2 = 5 4
C. V 1 V 2 = 5 6
D. V 1 V 2 = 6 5
Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và
S
A
S
B
S
C
a
. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; D là điểm đối xứng của S qua P. I là giao điểm của đường thẳng AD với mặt phẳng (SMN). Tính theo a thể tích của khối tứ diện MBSI. A.
a
3
12
.
B. ...
Đọc tiếp
Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và S A = S B = S C = a . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; D là điểm đối xứng của S qua P. I là giao điểm của đường thẳng AD với mặt phẳng (SMN). Tính theo a thể tích của khối tứ diện MBSI.
A. a 3 12 .
B. a 3 36 .
C. a 3 6 .
D. 2 a 3 12 .