Đáp án D
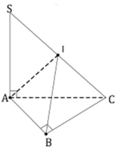

Lấy I là trung điểm của SC. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
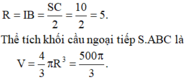
Đáp án D


Lấy I là trung điểm của SC. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
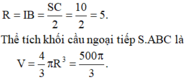
Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B với AB = 3; BC = 4. Hai mặt bên (SAB) và (SAC) cùng vuông góc với (ABC) và SC hợp với (ABC) góc 45 o . Tính thể tích hình cầu ngoại tiếp S.ABC.
A. V = 5 π 2 3
B. V = 25 π 2 3
C. V = 125 π 3 3
D. V = 125 π 2 3
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, AB = 3, BC = 4. Hai mặt phẳng (SAB), (SAC) cùng vuông góc với mặt phẳng đáy, đường thẳng SC hợp với mặt phẳng đáy một góc 45 ° . Thể tích mặt cầu ngoại tiếp hình chóp S.ABC là
A. V = 5 π 2 3
B. V = 25 π 2 3
C. V = 125 π 3 3
D. V = 125 π 2 3
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên S A B , S B C tạo với mặt đáy các góc bằng nhau và bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4 V = 3 a 3 12
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AC = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 ° .Tính theo a thể tích V của khối chóp S. ABC.
A. V = 3 a 3 2
B. V = 3 a 3 4
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B, A B = d . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 ° . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu .
A. 4 2 πa 3 3
B. 2 2 πa 3 3
C. 8 2 πa 3 3
D. 2 πa 3 3
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60 0 . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B với A B = 3 a , B C = 4 a , S A ⊥ A B C và cạnh bên SC tạo với đáy góc 60 ° . Tính thể tích khối cầu ngoại tiếp S.ABC.
A. V = 500 π a 3 3
B. V = 5 π a 3 3
C. V = 50 π a 3 3
D. V = π a 3 3
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V khối cầu ngoại tiếp hình chóp S.ABC
A. V = 4 3 π a 3 27
B. V = 5 15 π a 3 54
C. V = 5 15 π a 3 18
D. V = 5 π a 3 3