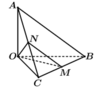
Đặt
O
A
=
O
B
=
O
C
= a suy ra 
Gọi N là trung điểm AC, ta có MN//AB. Khi đó 
Trong tam giác OMN có 
nên OMN là tam giác đều
Chọn C.
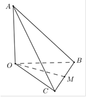
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Gọi M là trung điểm cạnh BC. Côsin góc giữa hai đường thẳng AB và OM bằng
A. 10 10
B. 10 5
C. 3 10 10
D. 15 5
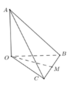
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 90 o
B. 30 o
C. 60 o
D. 45 o
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OB=OC. Gọi M là trung điểm BC,OM=a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng OA và BC bằng
A. 2 a.
B. 2 a.
C. 2 2 a.
D. 3 2 a.
Cho tứ diện O A B C có O A , O B , O C đôi một vuông góc với nhau và O B = O C Gọi M là trung điểm B C , O M = a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng OA và BC bằng
A. a.
B. 2 a.
C. a 2 2
D. a 3 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OC = 2a, OA = OB = a. Gọi M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng OM và AC
A. 2 a 3 .
B. 2 5 a 5 .
C. 2 a 3 .
D. 2 a 2 .
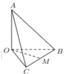
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và O A = O B = O C . Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng M và AB bằng
A. 60 0 .
B. 30 0 .
C. 60 0 .
D. 45 0 .
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng:
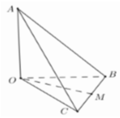
A. 90 ∘ .
B. 30 ∘ .
C. 60 ∘ .
D. 45 ∘ .
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng:
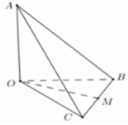
A. 90 °
B. 30 °
C. 60 °
D. 45 °
cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=OC=a. gọi I là trung điểm BC; H,K lần lượt là hình chiếu của O lên AB,AC.
1. Chứng minh:BC vuông góc (OAI), (OAI) vuông góc (OHK)
2. Tính d(O,(ABC))
3.Tính cosin (OA,(OHK))
4.Tính tan((OBC),(ABC))
5.Tìm đường vuông góc chung của HK,OI. tính khoảng cách giữa hai đường ấy
