BI = (a√3)/2 (đường cao tam giác đều)
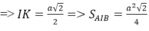
Đáp án C
BI = (a√3)/2 (đường cao tam giác đều)
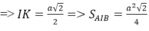
Đáp án C
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 . Chu vi thiết diện đó bằng:
A. a 3 + 1
B. a 2 3 + 1 2
C. 2 a 3 + 1
D. 2 a 3 + 3 2
Cho tứ diện đều ABCD cạnh bằng a. gọi trọng tâm các tam giác BCD, ACD lần lượt là G 1 , G 2 .
Tìm câu đúng nhất.
Thiết diện của hình tứ diện cắt bởi mặt phẳng ( B G 1 G 2 ) là:
A. Tam giác
B. Tứ giác
C. Tam giác cân
D. Hình thang
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 3 2 .
B. a 2 2 4 .
C. a 2 2 6 .
D. a 2 4 4 .
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 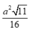
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A . a 2 11 2
B . a 2 2 4
C . a 2 11 4
D . a 2 3 4
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a. Gọi M và N lần lượt là trung điểm của AC và BC; P là trọng tâm tam giác BCD. Mặt phẳng (MNP) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 11 2 .
B. a 2 2 4 .
C. a 2 11 4 .
D. a 2 3 4 .
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD có tâm là điểm I. Gọi G(-1/3;0) và K(-1/3;-5/3) lần lượt là trọng tâm các tam giác ABI và ACD. Biết A(a;b) với a là số nguyên. Khi đó a^2+b^2 bằng bao nhiêu? giup em voi em cam on nhieu lammmm
Cho tứ diện ABCD có thể tích V . Gọi M, N, P, Q lần lượt là trọng tâm tam giác ABC, ACD, ABD và BCD . Thể tích khối tứ diện MNPQ bằng
A. 4 V 9
B. V 27
C. V 9
D. 4 V 27