Các câu hỏi tương tự
Cho tứ diện ABCD và các điểm M,N xác định bởi
A
M
→
2
A
B
→
−
3
A
C
→
;
D
N
→
D
B
→
+...
Đọc tiếp
Cho tứ diện ABCD và các điểm M,N xác định bởi A M → = 2 A B → − 3 A C → ; D N → = D B → + x D C → . Tìm x để ba véc tơ A D → , B C → , M N → đồng phẳng
A.x= -1
B. x= -3
C. x= -2
D. x= 2
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1),M(2;4;1),N(1;5;3). Tìm toạ độ điểm C nằm trên mặt phẳng (P):x+z-27=0 sao cho tồn tại các điểm B,D tương ứng thuộc các tia AM, AN để tứ giác ABCD là hình thoi.
A. C(6;-17;21).
B. C(20;15;7).
C. C(6;21;21).
D. C(18;-7;9).
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A), (B), (C), (D) giới hạn bởi đồ thị hàm số f(x) và trục hoành lần lượt bẳng 6; 3; 12; 2. Tích phân
∫
-
3
1
2
f
2
x
+
1
+...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên đoạn [-5;3] có đồ thị như hình vẽ bên. Biết diện tích các hình phẳng (A), (B), (C), (D) giới hạn bởi đồ thị hàm số f(x) và trục hoành lần lượt bẳng 6; 3; 12; 2. Tích phân ∫ - 3 1 2 f 2 x + 1 + 1 d x bằng
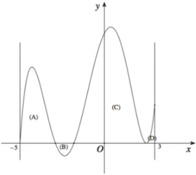
A. 27
B. 25
C. 17
D. 21
Cho hàm số
f
x
log
1
2
log
4
log
1
4
log
16
log...
Đọc tiếp
Cho hàm số f x = log 1 2 log 4 log 1 4 log 16 log 1 16 x . Tập xác định của f ( x) là D=(a;b) trong đó a và b là các số thực, b − a = m n , m và n là các số tự nhiên nguyên tố cùng nhau. Tìm tổng m + n.
A. 19
B. 31
C. 271
D. 319
Trong mặt phẳng tọa độ oxy Cho hình vuông ABCD có A (-2,0) điểm C nằm trên đường thẳng có pt X+Y-3=o ,M là trung điểm cạnh BC N nằm trên AD sao cho AN = 2 ND .tìm tọa đôj B,C,D .biết phương trình MN 7X-6Y-5=0
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
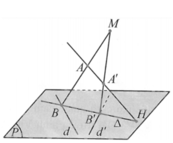
A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Cho đường thẳng d: 2x - y + 10 0 và điểm M(1; -3)a) Tính khoảng cách từ điểm M đến đường thẳng db) Viết pt đường thẳng đi qua M và vuông góc với đường thẳng dc) Viết pt tiếp tuyến với đường tròn (C): (x-2)2 + (y-3)2 9 biết rằng tiếp tuyến đó song song với đường thẳng dd) Cho ∆ABC biết tọa độ trực tâm H(2;2). Tâm đường tròn ngoại tiếp ∆ABC là điểm I(1;2). Xác định tọa độ các điểm A, B, C biết trung điểm của BC là điểm M(1;1) và hoành độ điểm B âm
Đọc tiếp
Cho đường thẳng d: 2x - y + 10 =0 và điểm M(1; -3)
a) Tính khoảng cách từ điểm M đến đường thẳng d
b) Viết pt đường thẳng đi qua M và vuông góc với đường thẳng d
c) Viết pt tiếp tuyến với đường tròn (C): (x-2)2 + (y-3)2 =9 biết rằng tiếp tuyến đó song song với đường thẳng d
d) Cho ∆ABC biết tọa độ trực tâm H(2;2). Tâm đường tròn ngoại tiếp ∆ABC là điểm I(1;2). Xác định tọa độ các điểm A, B, C biết trung điểm của BC là điểm M(1;1) và hoành độ điểm B âm
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
câu 1 : Trên nữa mặt phẳng đường tròn (O) đường kính AB ta lấy điểm M bất kỳ ( M khác A và B ), các tiếp tuyến tại M và B với nửa đường tròn cắt nhau ở C . Từ tâm O của nữa đường tròn ta kẻ đường thẳng song song với MB cắt các tiếp tuyến CM và CB lần lượt tại D và E .CM rằng :a) Tam giác CDE cânb) AD là tiếp tuyến của nữa đường tròn c) Khi M di chuyển trên nữa đường tròn thì tích AB . CD không thay đỗicâu 2 :cho các hàm số y2mx+3 và y (n-1)x-2a) biết rằng trên cùng một mặt phẳng tọa độ , dồ thị...
Đọc tiếp
câu 1 :
Trên nữa mặt phẳng đường tròn (O) đường kính AB ta lấy điểm M bất kỳ ( M khác A và B ), các tiếp tuyến tại M và B với nửa đường tròn cắt nhau ở C . Từ tâm O của nữa đường tròn ta kẻ đường thẳng song song với MB cắt các tiếp tuyến CM và CB lần lượt tại D và E .CM rằng :
a) Tam giác CDE cân
b) AD là tiếp tuyến của nữa đường tròn
c) Khi M di chuyển trên nữa đường tròn thì tích AB . CD không thay đỗi
câu 2 :
cho các hàm số y=2mx+3 và y = (n-1)x-2
a) biết rằng trên cùng một mặt phẳng tọa độ , dồ thị các hàm số này cắt nhau tại điểm A ( 1;-1). Hãy xác định m và n
b) Với các giá trị của m và n tìm được ở trên , hãy vẽ đồi thị của các hàm số tương ứng trên cùng một mặt phẳng tọa độ








