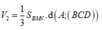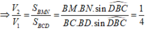Các câu hỏi tương tự
Cho tứ diện ABCD . Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện ABCD và khối tứ diện ABCD bằng:
A
.
1
8
B
.
1
6
C
.
1
4
D
.
1
2
Đọc tiếp
Cho tứ diện ABCD . Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AB'C'D' và khối tứ diện ABCD bằng:
A . 1 8
B . 1 6
C . 1 4
D . 1 2
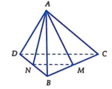
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD) Gọi
V
1
,
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD) Gọi V 1 , V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
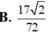
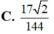
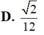
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho . Tính thể tích V của khối tứ diện PMNC
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho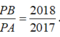 
. Tính thể tích V của khối tứ diện PMNC
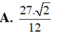
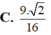
Cho hình lập phương ABCD. A ‘B’C’D’ có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, C’D’ và DD’. Tính thể tích khối tứ diện MNPQ A.
3
8
B.
1
8
C.
1
12
D.
1
24
Đọc tiếp
Cho hình lập phương ABCD. A ‘B’C’D’ có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, C’D’ và DD’. Tính thể tích khối tứ diện MNPQ
A. 3 8
B. 1 8
C. 1 12
D. 1 24
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA 3a, BC BD 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM A. V 8
a
3
B. V
2
a
3
3
C. V
3
a
3
2
D. V...
Đọc tiếp
Cho tứ diện ABCD có các cạnh BA, BC, BC đôi một vuông góc với nhau, BA = 3a, BC = BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 3 a 3 2
D. V = a 3
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, SD và BC. Gọi E là giao điểm của mặt phẳng (MNP) với cạnh SA. Tính tỉ số SE SA . A. 1 4 . B. 1 2 . C. 1 3 . D. 3
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB 6a, AC 7a, AD 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là: A. 14
a
2
. B. 28
a
2
. C. 42
a
2
. D. 7
a
2...
Đọc tiếp
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC= 7a, AD = 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2 .
B. 28 a 2 .
C. 42 a 2 .
D. 7 a 2 .
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng A.
11
2
216
B.
2
27
C. ...
Đọc tiếp
Cho tứ diện ABCD đều cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB, BC. Điểm P trên cạnh CD sao cho Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích của khối đa diện BMNPQD bằng
A. 11 2 216
B. 2 27
C. 5 2 108
D. 7 2 216