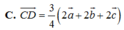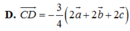Các câu hỏi tương tự
Cho tứ diện ABCD. Gọi
G
1
và
G
2
lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
Đọc tiếp
Cho tứ diện ABCD. Gọi G 1 và G 2 lần lượt là trọng tâm các tam giác BCD và ACD. Trong các khẳng định sau, khẳng định nào sai?
![]()
![]()
![]()
![]()
Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ. A.
2017
9
B.
4034
81
C.
8068
27
D.
2017
27
Đọc tiếp
Cho khối tứ diện ABCD có thể tích 2017. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.
A. 2017 9
B. 4034 81
C. 8068 27
D. 2017 27
Cho tứ diện ABCD. Xét điểm M thay đổi là một điểm trong của tứ diện. Gọi A,B,C,D lần lượt là giao điểm của các đường thẳng AM, BM, CM, DM với các mặt phẳng (BCD), (ACD), (ABD), (ABC). Giá trị nhỏ nhất của biểu thức
P
A
M
M
A
+
B
M
M
B...
Đọc tiếp
Cho tứ diện ABCD. Xét điểm M thay đổi là một điểm trong của tứ diện. Gọi A',B',C',D' lần lượt là giao điểm của các đường thẳng AM, BM, CM, DM với các mặt phẳng (BCD), (ACD), (ABD), (ABC). Giá trị nhỏ nhất của biểu thức P = A M M A ' + B M M B ' + C M M C ' + D M M D ' bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có DA vuông góc với mp(ABC),
A
D
A
B
B
C
a
,
D
B
⊥
B
C
. Kí hiệu
V
1
,
V
2
,
V
3
lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi...
Đọc tiếp
Cho tứ diện ABCD có DA vuông góc với mp(ABC), A D = A B = B C = a , D B ⊥ B C . Kí hiệu V 1 , V 2 , V 3 lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng ?
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
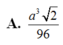
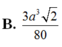
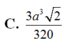
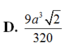
Cho tứ diện đều ABCD. Gọi E là trọng tâm tam giác BCD và F là trung điểm của AE. Gọi H là hình chiếu vuông góc của F trên đường thẳng AD. Đường thẳng FH cắt mặt phẳng (ABC) tại điểm M. Mệnh đề nào sau đây sai?
Đọc tiếp
Cho tứ diện đều ABCD. Gọi E là trọng tâm tam giác BCD và F là trung điểm của AE. Gọi H là hình chiếu vuông góc của F trên đường thẳng AD. Đường thẳng FH cắt mặt phẳng (ABC) tại điểm M. Mệnh đề nào sau đây sai?
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC), DB vuông góc BC, AD AB BC a. Kí hiệu V1, V2, V3 lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng? A.
V
1
V
2
V
3
B.
V...
Đọc tiếp
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC), DB vuông góc BC, AD = AB = BC = a. Kí hiệu V1, V2, V3 lần lượt là thể tích của hình tròn xoay sinh bởi tam giác ABD khi quay quanh AD, tam giác ABC khi quay quanh AB, tam giác DBC khi quay quanh BC. Trong các mệnh đề sau, mệnh đề nào đúng?
A. V 1 = V 2 = V 3
B. V 1 + V 2 = V 3
C. V 1 = V 2 + V 3
D. V 1 + V 3 = V 2
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
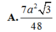
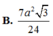
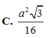
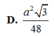
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt
x
→
A
B
→
,
y
→
A
C
→
,
z...
Đọc tiếp
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt x → = A B → , y → = A C → , z → = A D → . Khẳng định nào sau đây là khẳng định đúng?
A. A G → = 1 3 ( x → + y → + z → )
B. A G → = - 1 3 ( x → + y → + z → )
C. A G → = 2 3 ( x → + y → + z → )
D. A G → = - 2 3 ( x → + y → + z → )