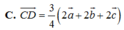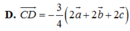Chọn D
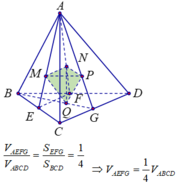
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
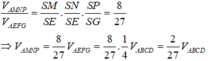
Do mặt phẳng (MNP) (BCD) nên
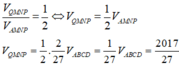
Chọn D

(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
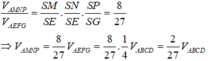
Do mặt phẳng (MNP) (BCD) nên
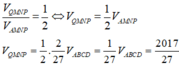
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
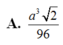
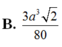
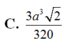
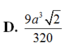
Cho hình lăng trụ A B C . A ' B ' C ' có thể tích bằng a 3 . Gọi M, N, P lần lượt là tâm của các mặt bên và G là trọng tâm tam giác ABC . Tính thể tích V của khối tứ diện GMNP.
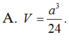
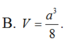
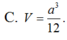
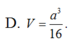
Cho hình lăng trụ ABCA'B'C' có thể tích bằng α 3 . Gọi M, N, P lần lượt là tâm của các mặt bên và G là trọng tâm tam giác ABC. Thể tích của khối tứ diện GMNP bằng
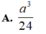
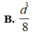
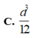
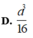
Cho tứ diện ABCD có BD=2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng 16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).
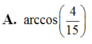

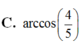
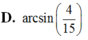
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD. Tính thể tích V của khối chóp A.GBC.
A. V = 3
B. V = 4
C. V = 6
D. V = 5
Cho tứ diện ABCD có C D = a 2 , ∆ A B C là tam giác đều cạnh a, ∆ A C D vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích của khối cầu ngoại tiếp tứ diện ABCD bằng
A. 4 πa 3 3
B. πa 3 6
C. 4 πa 3
D. πa 3 3 2
Cho tứ diện ABCD có thể tích V. Gọi G là trọng tâm tam giác ADC. Tính thể tích khối chóp G.ABC theo V.
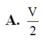
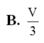
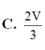
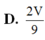
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD. Gọi A,B',C' lần lượt là trọng tâm các tam giác BCD, ACD, ABD. Đặt A A ' → = a → , B B ' → = b → , C C ' → = c → . Mệnh đề nào sau đây đúng?
![]()
![]()