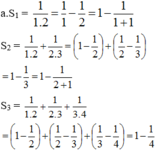
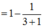
b. Dự đoán: 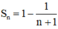
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
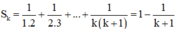
Khi đó:
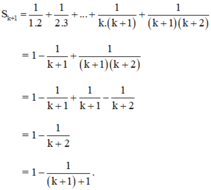
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
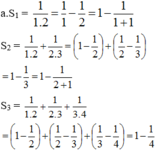
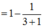
b. Dự đoán: 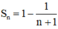
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
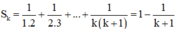
Khi đó:
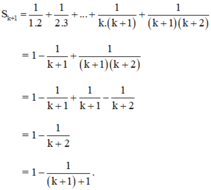
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*
Cho tổng: S n = 1 1 . 5 + 1 5 . 9 + . . . + 1 4 n - 3 4 n + 1
a) Tính S 1 , S 2 , S 3 , S 4 ;
b) Dự đoán công thức tính S n và chứng minh bằng phương pháp quy nạp.
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
Cho hai số 3 n và 8n với n ∈ N * .
a) So sánh 3 n và 8n khi n = 1 , 2 , 3 , 4 , 5 .
b) Dự đoán kết quả tổng quát và chứng minh bằng phương pháp quy nạp
Chứng minh công thúc Tổng của một cấp số nhân bằng phương pháp Quy nạp.
\(S_n=\dfrac{U_1\left(1-q^n\right)}{1-q}\)
Chứng minh Công thức sau bằng phương pháp Quy nạp.
\(S_n\)= \(\dfrac{u_1\left(1-q^n\right)}{1-q}\)
Cho dãy số \(\left(a_n\right)\) xác định bởi công thức:
\(\hept{\begin{cases}a_1=1;a_2=2;\\na_{n+2}=\left(3n+2\right)a_{n+1}-2\left(n+1\right)a_n;n=1;2;3...\end{cases}}\)
a) Tìm công thức số hạng tổng quát của dãy \(\left(a_n\right)\)
b)Chứng minh \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\frac{n\left(n+1\right)}{2};\forall n\inℕ^∗\)
c) Tính \(lim\left(\frac{a_1}{3}+\frac{a_2}{3^2}+...+\frac{a_n}{3^n}\right)\)
Chứng minh rằng:
\(n^n\ge\left(n+1\right)^{n-1}\forall n\inℕ^∗\)
Chứng minh bằng phương pháp quy nạp nhé
chứng minh rằng 3^n ≥ 2n+1 với mọi n thuộc N
làm đúng dạng quy nạp toán học mình tích cho
Cho dãy số u n , biết u 1 = - 1 , u n + 1 = u n + 3 v ớ i n ≥ 1 .
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: u n = 3 n – 4