Chọn B.
Phương pháp:
Sử dụng tính chất của tích phân:
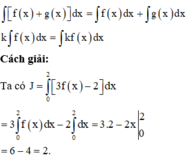
Chọn B.
Phương pháp:
Sử dụng tính chất của tích phân:
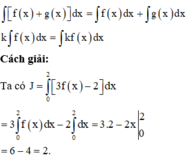
Xét hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn điều kiện f(1)=1 và f(2)=4.
Tính J = ∫ 1 2 f ' ( x ) + 2 x - f ( x ) + 1 x 2 d x
A. J = 1 + ln 4
B. J = 4 - ln 2
C. J = ln 2 - 1 2
D. J = 1 2 + ln 4
Xét hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn điều kiện f(1)=1 và f(2)=4 Tính J = ∫ 1 2 f ' x + 2 x - f x + 1 x 2 dx
A. J = 1 + ln 4
B. J = 4 - ln 2
C. J = ln 2 - 1 2
D. J = 1 2 + ln 4
Cho tích phân I = ∫ 0 4 f x d x = 32. Tính tích phân J = ∫ 0 2 f 2 x d x
A. J = 32
B. J = 64
C. J = 8
D. J = 16
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ] và thỏa mãn f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .
A. I = 2
B. I = - 2
C. I = 6
D. I = - 6
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Cho I = lim x → 0 2 x + 1 − 1 x và J = lim x → 1 x 2 + x − 2 x − 1 . Tính I+J
A. 3
B. 5
C. 4
D. 2
Cho I = lim x → 0 2 x + 1 − 1 x và J = lim x → 1 x 2 + x − 2 x − 1 . Tính I + J
A. 3.
B. 5
C. 4
D. 2.
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K)
Kẻ đường thẳng l vuông góc với d tại J, trên l lấy điểm M khác với điểm J. đường thẳng qua l vuông góc với MK cắt l tại N. chứng minh rằng KN ⊥ IM.