Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}=k^2\)
\(\dfrac{ac}{bd}=k^2\)
Do đó: \(\dfrac{a^2-c^2}{b^2-d^2}=\dfrac{ac}{bd}\)
Bài 7: Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng ta có các tỉ lệ thức sau( giả thiết các tỉ lệ thức phải chứng minh đều có nghĩa):
a)\(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\) b)\(\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
c)\(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\) d)\(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
ai hộ mik vs
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\) (Giả thiết các tỉ số đều có nghĩa). Chứng minh:
a) \(\dfrac{5a+2b}{5a-2b}=\dfrac{5c+2d}{5a-2d}\) b)\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
Từ tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\), (Các tỉ số đã viết đều có nghĩa). Chứng minh các tỉ lệ thức sau:
a) \(\dfrac{a}{b}=\dfrac{a+b}{c+d}\)
b)\(\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
Cho tỉ lệ thức \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) . Chứng minh rằng : \(\dfrac{a^2}{b^2}\) = \(\dfrac{c^2}{d^2}\) = \(\dfrac{ac}{bd}\)
Các bạn nhớ giải nhanh giúp mình nhé !
Ai làm nhanh nhất sẽ được tick 5 sao!!!
Cho các số a,b,c thỏa mãn .\(\text{ }\dfrac{1}{a+b}=\dfrac{2}{b+c}=\dfrac{3}{c+a}\)
giả thiết các tỉ số đều có nghĩa). Tính giá trị của Q=\(\dfrac{a+2021b+c}{a+2022b+c}\)
Cho \(\dfrac{a}{c}\)=\(\dfrac{b}{d}\)(giả thiết các tỉ số đều có nghĩa)
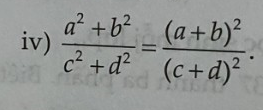
Cho tỉ lệ thức \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). Chứng minh rằng \(\dfrac{a.d}{c.d}=\dfrac{a^2-b^2}{b^2-d^2}\)và \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
Cho tỉ lệ thức\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). Chứng minh rằng ta có tỉ lệ sau: \(\dfrac{7a^2+3ab}{11a^2-8b^2}\)=\(\dfrac{7c^2+3cd}{11c^2-8d^2}\)
Cho tỉ lệ thức a/b=c/d Chứng minh rằng ac/a2+c2=bd/b2+d2
giả thiết các tỉ số đều có nghĩa
