Xét tứ giác ABDC có
F là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
=>BD=AC(1)
Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
=>CA=CK(2)
Từ (1) và (2) suy ra BD=AC=CK
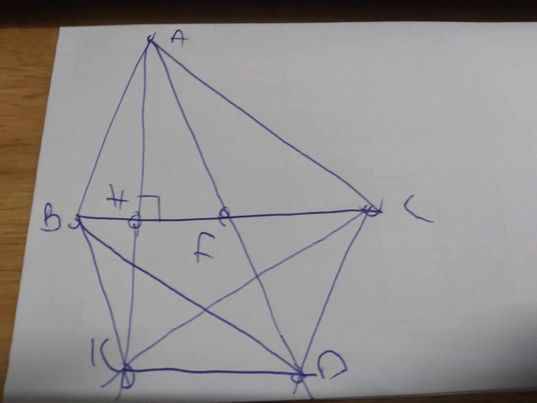
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh DK vuông góc với AH
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh AC song song với BD
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh AC song song với BD
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh AC song song BD
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD hãy vẽ hình
cho tam giác nhọn có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh tam giác ABF bằng tam giác DCF
cho tam giác nhọn ABC có AB nhỏ hơn AC lấy F là trung điểm của BC trên tia AF lấy điểm D sao cho F là trung điêm của AD chứng minh tam giác ABF bằng tam giác DCF
Cho tam giác ABC có đều nhọn ,AB<AC. Lấy E là trung điểm của BC .Trên tia AE lấy điểm D sao cho E là trung điểm của AD. Chứng minh:
a. tam giác ABE=tam giác DCE
b. AC//BD
c.Vẽ AH vuông góc với BC (H thuộc BC). Trên tia AH lấy điểm K sao cho H là trung điểm của AK. Chứng minh BD=AC=CK
d.Chứng minh DK vuông góc với AH
