Question

Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC.Trên MA lấy điểm D sao cho MD = MB

a. Hỏi tam giác MBD là tam giác gì?

b. So sánh hai tam giác BDA và BMC

c. Chứng minh rằng MA =MB + MC

d. CM $\frac{1}{MN}=\frac{1}{MB}+\frac{1}{MC}$( N là giao điểm của AM và BC )

Answer 1

Answer 2

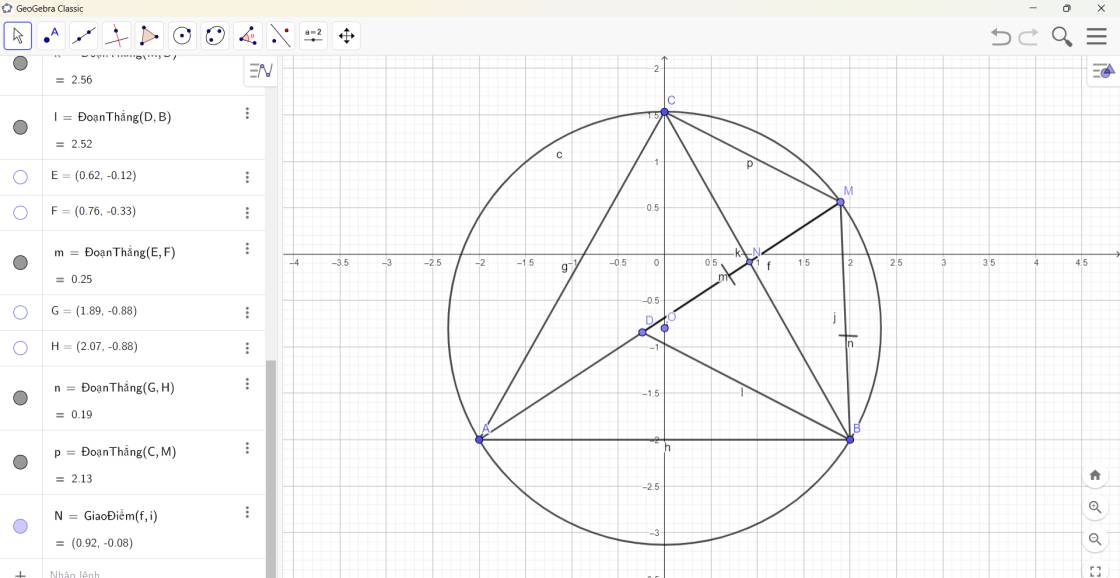
a: Xét (O) có

\(\widehat{AMB}\) là góc nội tiếp chắn cung AB

\(\widehat{ACB}\) là góc nội tiếp chắn cung AB

Do đó: \(\widehat{AMB}=\widehat{ACB}=60^0\)

Xét ΔMBD có MB=MD và \(\widehat{DMB}=60^0\)

nên ΔMBD đều

b: Xét (O) có

\(\widehat{BAM}\) là góc nội tiếp chắn cung BM

\(\widehat{BCM}\) là góc nội tiếp chắn cung BM

Do đó: \(\widehat{BAM}=\widehat{BCM}\)

Ta có: ΔDBM đều

=>DM=MB=DB và \(\widehat{DBM}=\widehat{DMB}=\widehat{MDB}=60^0\)

Ta có: \(\widehat{ABD}+\widehat{DBC}=\widehat{ABC}=60^0\)

\(\widehat{MBC}+\widehat{DBC}=\widehat{DBM}=60^0\)

Do đó: \(\widehat{ABD}=\widehat{MBC}\)

Xét ΔBAD và ΔBCM có

BD=BM

\(\widehat{ABD}=\widehat{CBM}\)

BA=BC

Do đó: ΔBAD=ΔBCM

c: Ta có: ΔBAD=ΔBCM

=>MC=DA

Ta có: MC+MB=DA+DM=MA