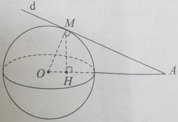
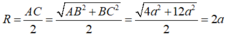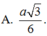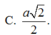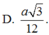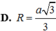Cho tam giác ABC vuông tại B và nằm trong mặt phẳng (P) có AB=2a, BC= 2 3 a . Một điểm S thay đổi trên đường thẳng vuông góc với (P) tại A ( S ≠ A ) . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Biết rằng khi S thay đổi thì bốn điểm A, B, H, K thuộc mặt cầu cố định. Tính bán kính R của mặt cầu đó.
A. R = 2 a
B. R = 3 a
C. R = 2 a
D. R = a
Chọn A.
Phương pháp:
Chỉ ra ba đỉnh H, K, B cùng nhìn cạnh AC dưới một góc vuông. Từ đó suy ra bán kính mặt cầu đi qua 4 điểm A, H, B, K.
Cách giải:
Ta có:
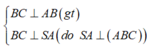
![]()
Mà:
![]()
![]()
Ta thấy:
![]()
Nên mặt cầu đi qua bốn đỉnh A; H; B; K nhận AC là đường kính nên bán kính: