Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
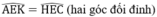
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)
Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
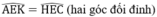
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)
: Cho tam giác ABC vuông tại A. Đường phân giác BE; kẻ EH vuông góc với BC ( H thuộc BC ). Gọi K là giao điểm của AB và HE. Chứng minh:
a/ EA = EH
b/ EK = EC
c/ BE vuông góc KC
Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi K là giao điểm của AB và HE Chứng minh : a) EA= EH b) EK= EC c) BE vuông góc KC
Cho tam giác ABC vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H thuộc BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) tam giác ABE = tam giác HBE
b) BE là đường trung trực của đoạn thẳng AH
c) EK = EC
d) Chứng minh AE < EC
Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi K là giao điểm của AB và HE , chứng minh rằng :
a , Tam giác ABE = tam giác HBE
b , BE lvuông góc AH
c , EK = EC
d , AE < EC
Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi K là giao điểm của AB và HE , chứng minh rằng :
a , Tam giác ABE = tam giác HBE
b , BE lvuông góc AH
c , EK = EC
d , AE < EC
Cho tam giác ABC vuông tại A; đường phân giác BE. Kẻ EH vuông góc với BC (H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:
AE < EC
Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi K là giao điểm của AB và HE , chứng minh rằng :
a , Tam giác ABE = tam giác HBE
b , BE là đường trung trực của đoạn thẳng AH
c , EK = EC
d , AE < EC
11) Cho tam giác ABC vuông tại A. Đường phân giác BE, kẻ EH vuông góc với BC( H thuộc BC. Gọi K là giao điểm của AB và HE. Chứng minh:
a) EA = EH
b) EK = EC
c) BE vuông góc với KC
Bài 9. Cho ABC vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng: a) ABE = HBE b) BE là đường trung trực của đoạn thẳng AH c) EK = EC d) Chứng minh AE < EC