Các câu hỏi tương tự
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH

cho tam giác abc vuông tại a(ab<ac), đường cao ah. gọi k là trung điểm ah. vẽ đường tròn tâm K, đường kính AH cắt ab và ac lần lượt tại d,e. a, chứng minh adhe là hình chữ nhật và ad.ab=ae.ac ; b, gọi O là trung điểm BC. Chứng minh AO vuông góc với DE. c, giả sử AB = 15cm, AC = 20cm. Trung trực của BC cắt nhau tại I. Tính bán kính đường tròn ngoại tiếp tứ giác BDEC
Cho tam giác ABC vuông ở A, đường cao AH chia cạnh huyền BC thành 2 đoạn ; BH,CH có độ dài lần lượt là 4cm và 9cm . Gọi D và E lần lượt là hình chiếu của điểm H trên AB và AC .Tính a, DE
b, Cắt đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N . chứng minh M là trung điểm của BH, N là trung điểm của CH.
c, Tính diện tích tứ giác DEMN
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB,AC. Biết AB4cm, AC6cm.a) Chứng minh : AD.ABAE.ACb) Tính độ dài AEc) Kẻ phân giác AI của góc BAC. Tính độ dài HId) Đường thẳng vuông góc với DE tại D cắt BC tại M. Chứng minh M là trung điểm của BHBài 2 : Cho tam giác ABC vuông ở A. Gỉa sử D là 1 điểm trên cạnh huyền BC và E.F lần lượt là hình chiếu của D lên các cạnh AB, AC. CMR : AE.EB + AF.FCBD.DC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E lần lượt là hình chiếu của H trên AB,AC. Biết AB=4cm, AC=6cm.
a) Chứng minh : AD.AB=AE.AC
b) Tính độ dài AE
c) Kẻ phân giác AI của góc BAC. Tính độ dài HI
d) Đường thẳng vuông góc với DE tại D cắt BC tại M. Chứng minh M là trung điểm của BH
Bài 2 : Cho tam giác ABC vuông ở A. Gỉa sử D là 1 điểm trên cạnh huyền BC và E.F lần lượt là hình chiếu của D lên các cạnh AB, AC. CMR : AE.EB + AF.FC=BD.DC
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia đối của tia AB lấy điểm K sao cho góc AKC = 600. D và E lần lượt là hình chiếu của H trên AB, AC. Qua A kẻ đường thẳng vuông góc với DE cắt BC tại M (M thuộc BC). Kẻ tia Cx là tia phân giác của góc ACB, qua M kẻ đường thẳng song song với AC cắt Cx tại F. Chứng minh BF vuông góc CF.
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH 9cm, CH 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ). Tính độ dài đoạn thẳng DE. A. DE 12cm B. DE 8cm C. DE 15cm D. DE 6cm
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
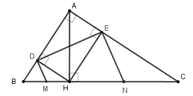
Tính độ dài đoạn thẳng DE.
A. DE = 12cm
B. DE = 8cm
C. DE = 15cm
D. DE = 6cm
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH 4cm, CH 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).Tính độ dài đoạn thẳng DE A. DE 5cm B. DE 8cm C. DE 7cm D. DE 6cm
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
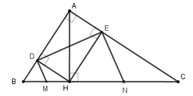
Tính độ dài đoạn thẳng DE
A. DE = 5cm
B. DE = 8cm
C. DE = 7cm
D. DE = 6cm
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH 4cm, CH 9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạch AB và AC a) Tứ giác ADHE là hình gì, tại sao? Tính DE b) Các đường thẳng vuông góc DE tại D và E lần lượt cắt BC tại M và N. C/m MN1/2BCc) Tính diện tích tứ giác DEMNd) C/m AD.ABAE.AC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 4cm, CH= 9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạch AB và AC
a) Tứ giác ADHE là hình gì, tại sao? Tính DE
b) Các đường thẳng vuông góc DE tại D và E lần lượt cắt BC tại M và N. C/m MN=1/2BC
c) Tính diện tích tứ giác DEMN
d) C/m AD.AB=AE.AC
cho tam giác ABC vuông tại A, đường cao AH. Gọi E và F lần lượt là hình chiếu vuông góc của H trên các cạnh AB,AC.Cho BH=3cm,CH=12cm.a) Tính độ dài các cạnh AB,AC.b)chứng minh:HF=2HE.c)Từ C kể đường thẳng vuông góc với BC,đường thẳng này cắt đường thẳng AB tại I,kẻ AK vuông góc với CI tại K.Chứng minh CI^3/CB^3=IK/BH
Xem chi tiết









