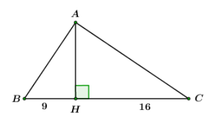
Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
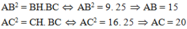
Xét ABC vuông tại A ta có:
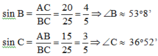
Đáp án cần chọn là: A

Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
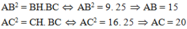
Xét ABC vuông tại A ta có:
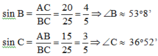
Đáp án cần chọn là: A
* Cho ΔABC có BC=12cm, góc B=\(60^0\), góc C=\(40^0\)
a. Tính đường cao CH và cạnh AC
b. Tính diện tích ΔABC (làm tròn đến chữ số thập phân thứ 2)
* Cho ΔABC vuông tại A có góc B= \(30^0\), AB=6cm
a. Giải tam giác vuông ABC
b. Vẽ đường cao AH, trung tuyến AM của ΔABC. Tính diện tích ΔAHM
Cho tam giác ABC vuông tại A , đường cao Ah .Biết HB = 25 cm, hc=64 cm .Tính góc B và góc C cua tam giác trên.
cho tam giác ABC vuông tại A và đường cao AH
a) Biết HB=4 , HC=9. Giải tam giác ABC
b) Biết AB=6 , góc B=53 độ . giải tam giác ABC
c) E,F lần lượt là hình chiếu của H trên AB,AC,CM. Tam giác EHF là hình chữ nhật và AH=EF
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB= 25cm, HC= 64cm. Tính AH, AC, góc B và góc C
Cho tam giác ABC vuông tại A có đường cao AH, trung tuyến AM, AB<AC.
a) Chứng minh AB^2/AC^2=HB/HC
b) Cho HC/HB=3, AM= 1cm. Tính góc ACB và diện tích tam giác AHM.
c) Biết rằng AH/AM=40/41 và AD là đường phân giác trong. Tính tỉ số DC/DB.
d) Giả sử sinB=1/3. Chứng minh cos2B=7/9.
Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:
( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2
Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:
( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2
Cho tam giác ABC vuông tại A đường cao AH tia phân giác góc B cắt AC tại D . biết DA=2cm DC=3cm.
a) Tính góc B góc C
b) Tính độ dài của AH; HB; HC