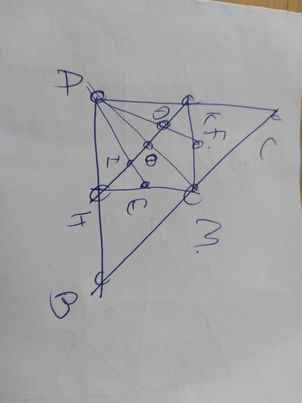
cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ MH, MK lần lượt vuông góc với AB và AC ( H thuộc AB và K thuộc AC)
a) chứng minh tứ giác AHKM là hình chữ nhật và AM = HK
b) chứng minh tứ giác BHKM là hình bình hành
c) gọi E là trung điểm của MH, F là trung điểm của MK. Đường thẳng HK cắt AE, À lần lượt tại I và D. Chứng minh HI = KD
Vẽ cả hình
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
=>AM=HK
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
M,K lần lượt là trung điểm của CB,CA
=>MK là đường trung bình của ΔABC
=>MK//AB và \(MK=\dfrac{AB}{2}\)
Ta có: MK//AB
H\(\in\)AB
Do đó: MK//HB
Ta có: \(MK=\dfrac{AB}{2}\)
\(AH=HB=\dfrac{AB}{2}\)
Do đó: MK=AH=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
c: Gọi O là giao điểm của AM và KH
Ta có: AHMK là hình chữ nhật
=>AM cắt KH tại trung điểm của mỗi đường
=>O là trung điểm của AM và KH
=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)
mà AM=KH
nên OA=OM=OK=OH(1)
Xét ΔAKM có
AF,KO là các đường trung tuyến
AF cắt KO tại D
Do đó: D là trọng tâm của ΔAKM
Xét ΔAKM có
D là trọng tâm
KO là đường trung tuyến
Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)
Xét ΔHAM có
AE,HO là các đường trung tuyến
AE cắt HO tại I
Do đó: I là trọng tâm của ΔHAM
Xét ΔHAM có
HO là đường trung tuyến
I là trọng tâm
Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)
Từ (1),(2),(3) suy ra HI=KD