Question

cho tam giác abc vuông tại a có bd là phân giác của góc abc ( dthuộc ac ) trên cạnh bc lấy điểm e sao cho be=ba cm tam giác abd = tam giác ebd b> họi o là giao điểm của ae và bd cm oa=oe

Answer 1

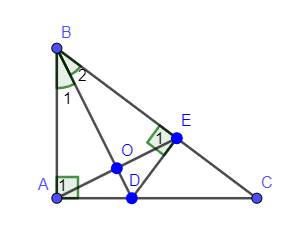
a: Xét ΔBAD và ΔBED co

BA=BE

góc ABD=góc EBD

BD chung

=>ΔBAD=ΔBED

b: ΔBAE cân tại B

mà BOlà phân giác

nên O là trung điểm của AE

=>OA=OE

Answer 2

`a)`

Có `BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`

Xét `Delta ABD` và `Delta EBD` có :

`{:(hat(BAD)=hat(BED)(=90^0)),(BD-chung),(hat(B_1)=hat(B_2)(cmt)):}}`

`=>Delta ABD=Delta EBD(c.h-g.n)(đpcm)`

`b)`

Có `Delta ABD=Delta EBD(cmt)`

`=>AB=BE` ( 2 cạnh t/ứng )

`=>Delta ABE` cân tại `B`

`=>hat(A_1)=hat(E_1)`

Xét `Delta ABO` và `Delta EBO` có :

`{:(hat(B_1)=hat(B_2)(cmt)),(BA=BE(cmt)),(hat(A_1)=hat(E_1)(cmt)):}}`

`=>Delta ABO=Delta EBO(g.c.g)`

`=>AO=EO` ( 2 cạnh t/ứng ) ( đpcm )